2021北师大五年级数学上册教案思维导图
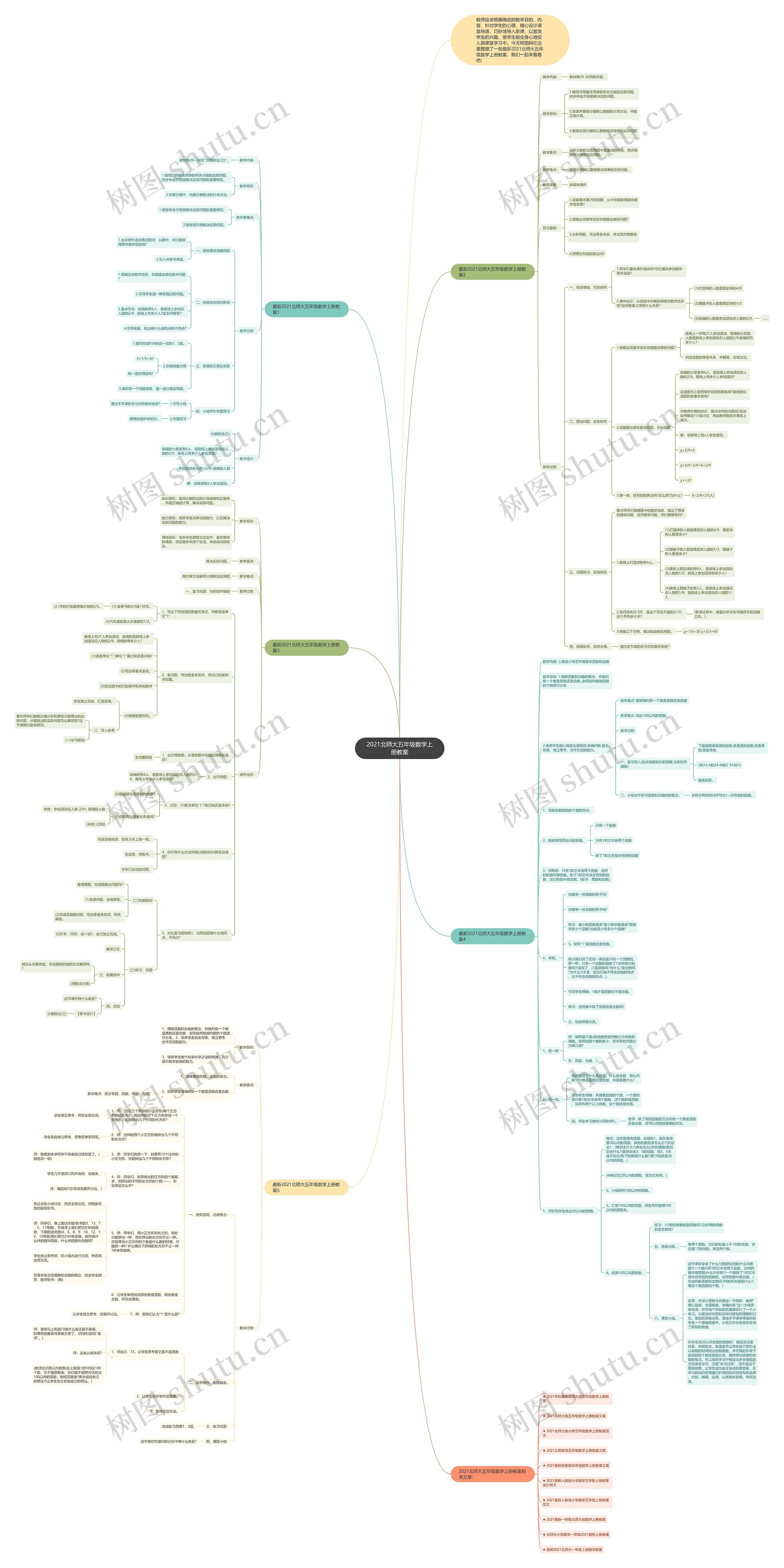
本模板介绍了2021北师大五年级数学上册教案思维导图中的知识点,教师应该根据确定的教学目的、内容,针对学生的心理,精心设计课堂导语,巧妙地导入新课,以激发学生的兴趣,使学生能全身心地投入到课堂学习中。本模板列举了两个最新的教案,其中包含到分数除法的计算方法和应用题的解答,教师要引导学生分析分数除法应用题中数量间的关系,用方程解答分数除法应用题,并能够运用分数除以整数解决简单的实际问题,通过本次的学习,学生能够初步体会方程是解决实际问题的重要模型。
思维导图大纲
2021北师大五年级数学上册教案思维导图模板大纲
教师应该根据确定的教学目的、内容,针对学生的心理,精心设计课堂导语,巧妙地导入新课,以激发学生的兴趣,使学生能全身心地投入到课堂学习中。今天树图网在这里整理了一些最新2021北师大五年级数学上册教案,我们一起来看看吧!
最新2021北师大五年级数学上册教案1
教学内容:
教材第29~30页"分数除法(三)"。
教学目标:
1.能用方程解决简单的有关分数的实际问题,初步体会方程是解决实际问题的重要模型。
2.在解方程中,巩固分数除法的计算方法。
教学重难点:
1.能够体会方程是解决实际问题的重要模型。
2.能够用方程解决实际问题。
教学过程:
一、创设情景激趣揭题
1.出示课外活动情况图问:从图中,你们能获得哪些数学信息呢?
2.引入并板书课题。
二、扶放结合探究新知
1.根据这些数学信息,你能提出哪些数学问题?
2.引导学生逐一解答提出的问题。
3.重点引导:跳绳的有6人,是操场上参加总人数的2/9,操场上有多少人?该怎样解答?
4.引导观察,找出有什么相同点和不同点?
三、反馈矫正落实双基
1.指导完成P29的试一试的1,2题。
2.你能根据方程
X×1/5=30
编一道应用题吗?
3.请你想一个问题情景,遍一道分数应用题。
四、小结评价布置预习
1.引导小结
通过本节课的学习你有哪些收获?
2.布置预习
整理前面所学知识。
板书设计:
分数除法(三)
跳绳的小朋友有6人,是操场上参加活动总人数的2/9,操场上有多少人参加活动?
参加活动总人数×2/9=跳绳的人数
解:设操场有X人参加活动。
最新2021北师大五年级数学上册教案2
教学内容:
教材第29-30页的内容。
教学目标:
1.能用方程解决简单的有关分数的实际问题,初步体会方程是解决实际问题。
2.探索并掌握分数除以整数的计算方法,并能正确计算。
3.能够运用分数除以整数解决简单的实际问题。
教学重点:
分析分数除法应用题中数量间的关系,用方程解答分数除法应用题。
教学难点:
运用分数除以整数解决简单的实际问题。
教具准备:
多媒体课件
预习提纲:
1.观察课本第29页的图,从中你能获得哪些数学信息呢?
2.根据这些数学信息你能提出哪些问题?
3.分析例题,写出等量关系,并试用方程解答。
4.想想还有别的算法吗?
教学过程:
一、创设情境,引发探究
1.同学们喜欢课外活动吗?你们喜欢参加哪些课外活动?
2.课件出示:从画面中你能获得哪些数学信息呢?这些数量之间有什么关系?
(1)打篮球的人数是踢足球的4/9.
(2)踢毽子的人数是踢足球的1/3.
(3)跳绳的人数是参加活动总人数的2/9.
……
二、提出问题,自主探究
1.根据这些数学信息你能提出哪些问题?
操场上一共有27人参加活动,跳绳的小朋友人数是操场上参加活动总人数的2/9.跳绳的有多少人?
列出这题的等量关系,并解答。全班交流。
2.还能提出哪些数学问题,引出例题
跳绳的小朋友有6人,是操场上参加活动总人数的2/9。操场上有多少人参加活动?
这道题与上题有哪些区别和联系呢?能找到这道题的数量关系吗?
你能用方程的知识,解决这样的问题吗?应该如何解设?小组讨论,再由教师指名在黑板上演示。
解:设操场上有x人参加活动。
χ×2/9=6
χ×2/9÷2/9=6÷2/9
χ×=27
3.想一想,还有别的算法吗?怎么算?为什么?
6÷2/9=27(人)
三、巩固练习,实践探究
刚才同学们根据图中的数学信息,提出了很多的数学问题,这些数学问题,你们能解答吗?
1.操场上打篮球的有4人。
(1)打篮球的人数是踢足球人数的4/9,踢足球的人数是多少?
(2)踢毽子的人数是踢足球人数的1/3,踢毽子的人数是多少?
(3)操场上踢足球的有9人,是操场上参加活动总人数的1/3,操场上参加活动有多少人?
(4)操场上踢毽子的有3人,是操场上参加活动总人数的1/9,是操场上参加活动总人数的1/3。
2.某月双休日 9天,是这个月总天数的3/10,这个月有多少天?
(板演过程中,着重分析学生可能存在的误解之处。)
3.根据以下方程,编出相应的应用题。
χ×1/5=30 χ×2/3=40
四、回顾反思,总结全课。
通过这节课的学习你有哪些收获?
最新2021北师大五年级数学上册教案3
教学目标:
知识目标:提高分数除法的计算速度和正确率,并能正确的计算,解决实际问题。
能力目标:培养学生动手动脑能力,以及解决实际问题的能力。
情感目标:培养学生愿意交流合作,喜欢数学的情操,感受数学来源于生活,体验成功的欢乐。
教学重点:
解决实际问题。
教学难点:
用方程方法解答分数除法应用题
教学过程:
一、复习巩固,为新知作铺垫
课件出示:
1、写出下列各题的数量关系式,判断谁是单位"1"
(1) 故事书的3/5是150本。
(2 )书的价钱是钢笔价钱的2/5。
(3)汽车速度是火车速度的1/2。
2、复习题:写出数量关系式,找出已知量和未知量。
操场上有27人参加活动,跳绳的是操场上参加活动总人数的2/9,跳绳的有多少人?
(1)谁是单位"1";单位"1"是已知还是未知?
(2)写出等量关系式。
(3)找出题中的已知条件和未知条件
(4)根据题意列式。
学生独立完成,汇报反馈。
二、导入新课
看来同学们都能正确分析和解答分数乘法的实际问题,分数除法的实际问题怎么解答呢?这节课我们就来研究。
(一)学习新知
1、出示情景图:从情景图中你能获得哪些信息?
生简要回答
2、出示例题:
跳绳的有6人,是操场上参加活动总人数的2/9,操场上有多少人参加活动?
3、讨论:(1)谁为单位"1"?是已知还是未知?
(2)根据那句话得到的信息?
(3)你能列出等量关系是吗?
半数:参加活动总人数-2/9= 跳绳的人数
(未知) (已知)
4、你们有什么办法利用以前的知识解答这道题?
同桌互相说说,在练习本上做一做。
生反馈,师板书。
学生口头检验对错。
5、对比复习题和例1,这两道题有什么相同点,不同点?
(二)巩固新知
看情景图,你还能提出问题吗?
(1)生提问题,全班解答。
(2)同桌互相提问题,写出等量关系式,列式解答。
(三)练习、巩固
打开书,29页,试一试1,自己独立完成。
集体订正
三、拓展延伸
回过头来看例题,你还能用其他的方法解答吗?
(用除法计算)
四、总结
这节课你有什么收获?
【板书设计】
分数除法(三)
最新2021北师大五年级数学上册教案4
教学内容: 人教版小学五年级数学质数和合数
教学目标: 1.理解质数和合数的概念,并能判断一个数是质数还是合数,,会把自然数按因数 的个数进行分类.
2.培养学生细心观察全面概括.准确判断.自主探索、独立思考、合作交流的能力。
教学重点: 能准确判断一个数是质数还是合数.
教学难点: 找出100以内的质数.
教学过程:
一、复习导入(加深前面知识的理解,为新知作铺垫)
下面各数谁是谁的因数,谁是谁的倍数,谁是偶数,谁是奇数.
3和15 4和24 49和7 91和13
指名回答。
二、小组合作学习质数和合数的的概念。
全班分两组探讨并写出1~20各数的因数。
1、观察各数因数的个数的特点。
2、板前填写师出示的表格。
只有一个因数
只有1和它本身两个因数
除了1和它本身还有别的因数
3、师概括:只有1和它本身两个因数,这样的的数叫做质数。除了1和它本身还有别的因数,这们的数叫做合数。(板书:质数和合数)
4、举例。
你能举一些质数的例子吗?
你能举一些合数的例子吗?
练习:最小的质数是谁?最小的合数是谁?质数有多少个因数?合数至少有多少个因数?
5。探究"1"是质数还是合数。
刚才我们说了还有一类就是只有一个因数的。想一想:只有一个因数的数除了1还有其它的数吗?(没有了,)1是质数吗?为什么?是合数吗?为什么?(不是,因为它既不符合质数的特点,也不符合合数的特点。)
引导学生明确:1既不是质数也不是合数。
练习:自然数中除了质数就是合数吗?
三、给自然数分类。
1、想一想
师:按照是不是2的倍数把自然数分为奇数和偶数。按照因数个数的多少,把非零自然数分为哪几类?
生:质数,合数,1。
2、说一说。
既然知道了什么是质数,什么是合数,那么判断一个数是质数还是合数,关键是看什么?
引导学生明确:关键看因数的个数,一个数如果只有1和它本身两个因数,这个数就是质数,如果有两个以上因数,这个数就是合数。
四、师生学习教材24页的例1。
老师:除了用找因数的方法判断一个数是质数还是合数,还可以用查质数表的方法。
1、师引导学生找出30以内的质数。
提问:这些数里有质数、合数和1,现在要保留30以内的质数,其他的数应该怎么办?(先划去1,)再划去什么?(再划去2以外的偶数)最后划去什么?(最后划去3、5的倍数,但3、5本身不划去)剩下的都是什么数?(剩下的就是30以内的质数。)
(特殊记忆20以内的质数,因为它常用。)
2。小组探究100以内的质数。
3。汇报100以内的质数。师生共同整理100以内的质数表。
4。应用100以内质数表:
练习:(1)有的奇数都是质数吗?(2)所有的偶数都是合数吗?
五、思维训练。
有两个质数,它们的和是小于100的奇数,并且是17的倍数。求这两个数。
六、课堂小结。
这节课你学会了什么?(质数和合数)什么叫质数?(一个数只有1和它本身两个因数,这样的数叫做质数)什么叫合数?(一个数除了1和它本身外还有别的因数的,这样的数叫做合数。)你会判断质数和合数吗?判断的关键是什么?(看这个数因数的个数。)
反思:在设计质数与合数这一节课时,我用"细心观察、全面概括、准确判断"这一主线贯穿全课。并在每个新知的后面都设计了一个小练习。以便及时巩固和加深对新知的理解和记忆。最后的思维训练,是给本节课学得很好的学生一个思维的提升。小结又针对全班学生做了新知的概括。
在学生找20以内各数的因数时,我应该注重探索,体现自主。就是放手让学生自己想办法以最短的时间找出各数因数,并在我的引导下按因数的个数给各数分类,最终得出质数和合数的概念。在以后的学习中我应当多多提倡自主探索性学习,注重"学习过程",而不是急于看到结果。让学生成为自主自动的思想家,在学习新知识时根据已积累的知识经验有所选择、判断、解释、运用,从而有所发现、有所创造。
最新2021北师大五年级数学上册教案5
教学目标:
1、理解质数和合数的概念,并能判断一个数是质数还是合数,会把自然数按约数的个数进行分类。2、培养学生自主探索、独立思考、合作交流的能力。
3、培养学生敢于探索科学之谜的精神,充分展示数学自身的魅力。
教学重点:
1、理解掌握质数、合数的概念。
2、初步学会准确判断一个数是质数还是合数。
教学难点:区分奇数、质数、偶数、合数。
教学过程:
一、探究发现,总结概念:
1、师:(出示三个同样的小正方形)每个正方形的边长为1,用这样的三个正方形拼成一个长方形,你能拼出几个不同的长方形?
学生独立思考,然后全班交流。
2、师:这样的四个小正方形能拼出几个不同的长方形?
学生各自独立思考,想像后举手回答。
3、师:同学们再想一下,如果有12个这样的小正方形,你能拼出几个不同的长方形?
师:我看到许多同学不用画就已经知道了。(指名说一说)
4、师:同学们,如果给出的正方形的个数越多,那拼出的不同的长方形的个数——,你觉得会怎么样?
学生几乎是异口同声地说:会越多。
师:确定吗?(引导学生展开讨论。)
5、师:同学们,用小正方形拼长方形,有时只能拼出一种,有时拼出的长方形不止一种。你觉得当小正方形的个数是什么数的时候,只能拼一种? 什么情况下拼得的长方形不止一种?并举例说明。
先让学生小组讨论,然后全班交流,师根据学生的回答板书。
师:同学们,像上面这些数(板书的3、13、7、5、11等数),在数学上我们把它们叫做质数,下面的这些数(4、6、8、9、10、12、14、15等数)我们把它们叫做合数。那究竟什么样的数叫质数,什么样的数叫合数呢?
学生独立思考后,在小组内进行交流,然后再全班交流。
引导学生总结质数和合数的概念,结合学生回答,教师板书:(略)
6、让学生举例说说哪些数是质数,哪些数是合数,并说出理由。
7、师:那你们认为"1"是什么数?
让学生独立思考,后展开讨论。
二、动手操作,制质数表。
1、师出示:73。让学生思考着它是不是质数。
师:要想马上知道73是什么数还真不容易。如果有质数表可查就方便了。(同学们都说"是呀"。)
师:这表从哪来呢?
(教师出示百以内数表)这上面是1到100这100个数,它不是质数表,你们能不能想办法找出100以内的质数,制成质数表?谁来说说自己的想法?(让学生充分发表自己的想法。)
2、让学生动手制作质数表。
3、集体交流方法。
三、练习巩固:
完成练习四第1、2题。
四、课题小结:
这节课你在激烈的讨论中有什么收获?
2021北师大五年级数学上册教案相关文章:
★ 2021年秋最新北师大版五年级数学上册教案
★ 2021北师大版五年级数学上册教案文案
★ 2021北师大版小学五年级数学上册教案范文
★ 2021义务教育五年级数学上册教案文案
★ 2021最新苏教版五年级数学上册教案文案
★ 2021最新人教版小学数学五年级上册教案设计例文
★ 2021最新人教版小学数学五年级上册教案范文
★ 2021最新一年级北师大版数学上册教案
★ 北师大小学数学一年级2021最新上册教案
★ 最新2021北师大一年级上册数学教案
相关思维导图模板


树图思维导图提供 北师大版五年级数学上册全册教案范文 在线思维导图免费制作,点击“编辑”按钮,可对 北师大版五年级数学上册全册教案范文 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c43e106b1ef63035126b7a61d60424d1


树图思维导图提供 2022年秋北师大版五年级数学上册教案 在线思维导图免费制作,点击“编辑”按钮,可对 2022年秋北师大版五年级数学上册教案 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0e4ce53fe82db2197fa30fda21dd40f4
















 上海工商
上海工商