高一数学各知识点解题技巧口诀：集合与函数思维导图

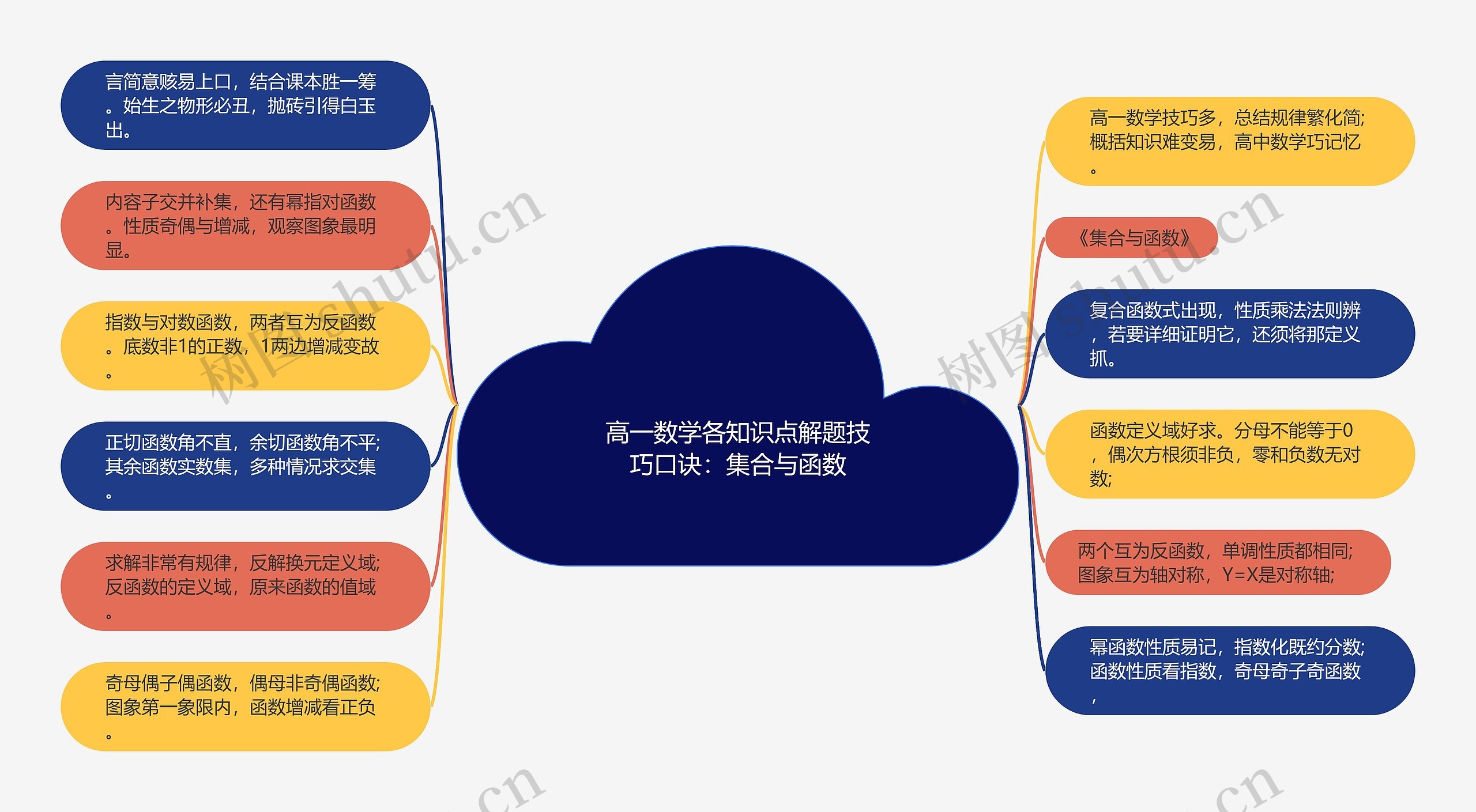
在高一数学中，集合与函数是重要的内容，下面是一些解题技巧和口诀：我们可以用模板大纲来总结和简化高一数学的规律。而且，要结合课本来学习，因为初学时的知识可能比较难理解，在解题过程中，需要注意集合的交并补集和幂指对函数，我们也要了解函数的性质，比如奇偶性和增减性，图象观察是最清晰的方式。当遇到复合函数时，要识别乘法法则，需要详细讨论定义的抓取，指数和对数函数是互为反函数的，底数非1的正数，当增减变化时，需要注意，函数的定义域可以很容易地求得，但是需要注意分母不等于0，偶次方根为非负数，而对数函数不能对零和负数取对数。正切函数的角不直，余切函数的角不平，其他函数的实数集，有多种情况需要求交集，如果两个函数互为反函数，他的单调性质是相同的，他的图象是轴对称的，轴对称轴是Y=X。在求解问题时，有一些规律可循，可以进行反解、换元和定义域的转换，反函数的定义域是原来函数的值域，幂函数的性质易于记忆，可以将指数化为最简分数。函数的性质可以通过指数来观察，奇母奇子为奇函数，奇母偶子为偶函数，偶母非奇偶函数，在函数的第一象限内，函数的增减可以看正负。