高二数学备考：数学解析几何中求参数取值范围的方法二思维导图
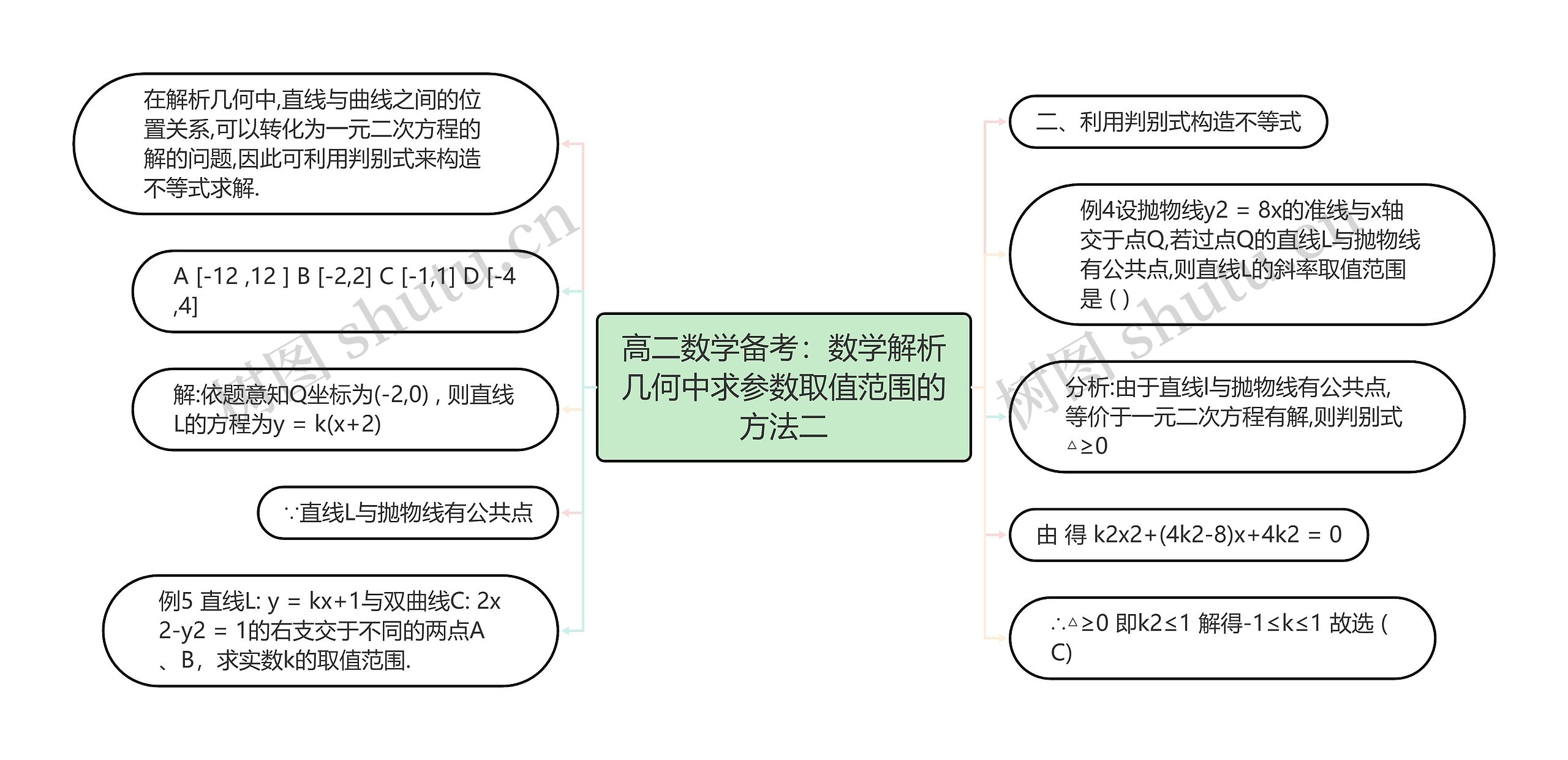
高二数学备考：数学解析几何中求参数取值范围的方法二思维导图模板大纲包含了利用判别式构造不等式的知识点，在解析几何中，直线与曲线之间的位置关系可以转化为一元二次方程的解的问题，因此可以利用判别式来构造不等式求解。举例来说，设抛物线y^2=8x/的准线与x轴交于点Q，若过点Q的直线L与抛物线有公共点，那么直线L的斜率取值范围，()。根据题意，直线L的方程可以表示为y=k/(x+2)，在通过对一元二次方程进行判别式的求解，可以得到斜率k的取值范围为[-1,1]，类似地，在例5中，根据方程y=kx+1与双曲线2x^2-y^2=1/的右支有两个不同交点A、B，需要求实数k的取值范围。
思维导图大纲
高二数学备考：数学解析几何中求参数取值范围的方法二思维导图模板大纲
二、利用判别式构造不等式
在解析几何中,直线与曲线之间的位置关系,可以转化为一元二次方程的解的问题,因此可利用判别式来构造不等式求解.
例4设抛物线y2 = 8x的准线与x轴交于点Q,若过点Q的直线L与抛物线有公共点,则直线L的斜率取值范围是 ( )
A [-12 ,12 ] B [-2,2] C [-1,1] D [-4,4]
分析:由于直线l与抛物线有公共点,等价于一元二次方程有解,则判别式△≥0
解:依题意知Q坐标为(-2,0) , 则直线L的方程为y = k(x+2)
由 得 k2x2+(4k2-8)x+4k2 = 0
∵直线L与抛物线有公共点
∴△≥0 即k2≤1 解得-1≤k≤1 故选 (C)
例5 直线L: y = kx+1与双曲线C: 2x2-y2 = 1的右支交于不同的两点A、B，求实数k的取值范围.
相关思维导图模板
树图思维导图提供 高考数学知识点实用 在线思维导图免费制作，点击“编辑”按钮，可对 高考数学知识点实用 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：f2e0583b31071d22a8fd080d40e0b9b8
树图思维导图提供 2023高考数学知识点 在线思维导图免费制作，点击“编辑”按钮，可对 2023高考数学知识点 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：67e43c5f03e398f10383430b79cdeb20
沪公网安备 31011502019485号
上海工商