高考数学考场答题技巧：三角函数及解三角形解题方法思维导图

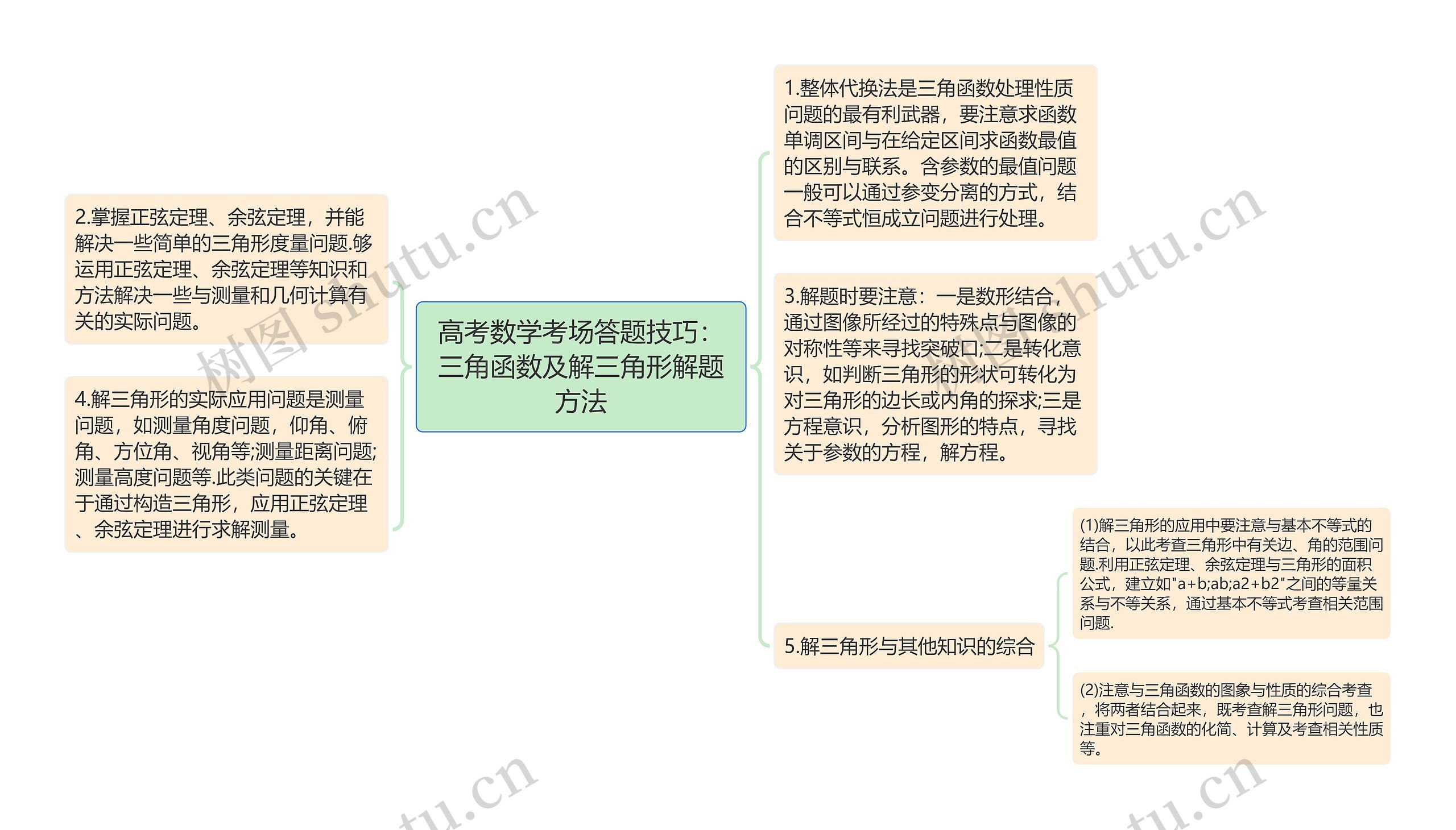
在高考数学考场答题中，掌握三角函数的处理性质是至关重要的，整体代换法是处理这类性质问题的最有效的方法，要注意区分求函数的单调区间和最值的区间，对于含参数的最值问题，可以通过参变分离的方式结合不等式恒成立问题进行处理。正弦定理和余弦定理是必须掌握的重要知识，能够用来解决三角形的度量问题。在解题过程中，需要注意数形结合，通过图像的特殊点和对称性来寻找突破口，转化意识，如判断三角形的形状可以转化为对边长或内角的探求，方程意识，分析图形的特点，寻找关于参数的方程并解方程。解三角形的实际应用问题包含测量问题，如测量角度、距离和高度，在解决这类问题时，关键在于构造三角形，并应用正弦定理和余弦定理进行求解测量，解三角形问题还会与其他知识进行综合，如基本不等式和三角函数的图像与性质的综合考查，通过建立等量关系和不等关系，和化简、计算和考查相关性质，可以进一步提高解题能力。