二元一次方程求根公式思维导图
有很多的同学是非常想知道,这个二元一次方程求根公式是什么呢,为了方便大家学习借鉴,下面小编精心准备了二元一次方程求根公式内容,欢迎使用学习!二元一次方程求根公式二元一次方程没有求根公式。
树图思维导图提供 二元一次方程求根公式 在线思维导图免费制作,点击“编辑”按钮,可对 二元一次方程求根公式 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:b49097f3ac1c77d9117b422df395e716
思维导图大纲
二元一次方程求根公式思维导图模板大纲
二元一次方程求根公式是什么
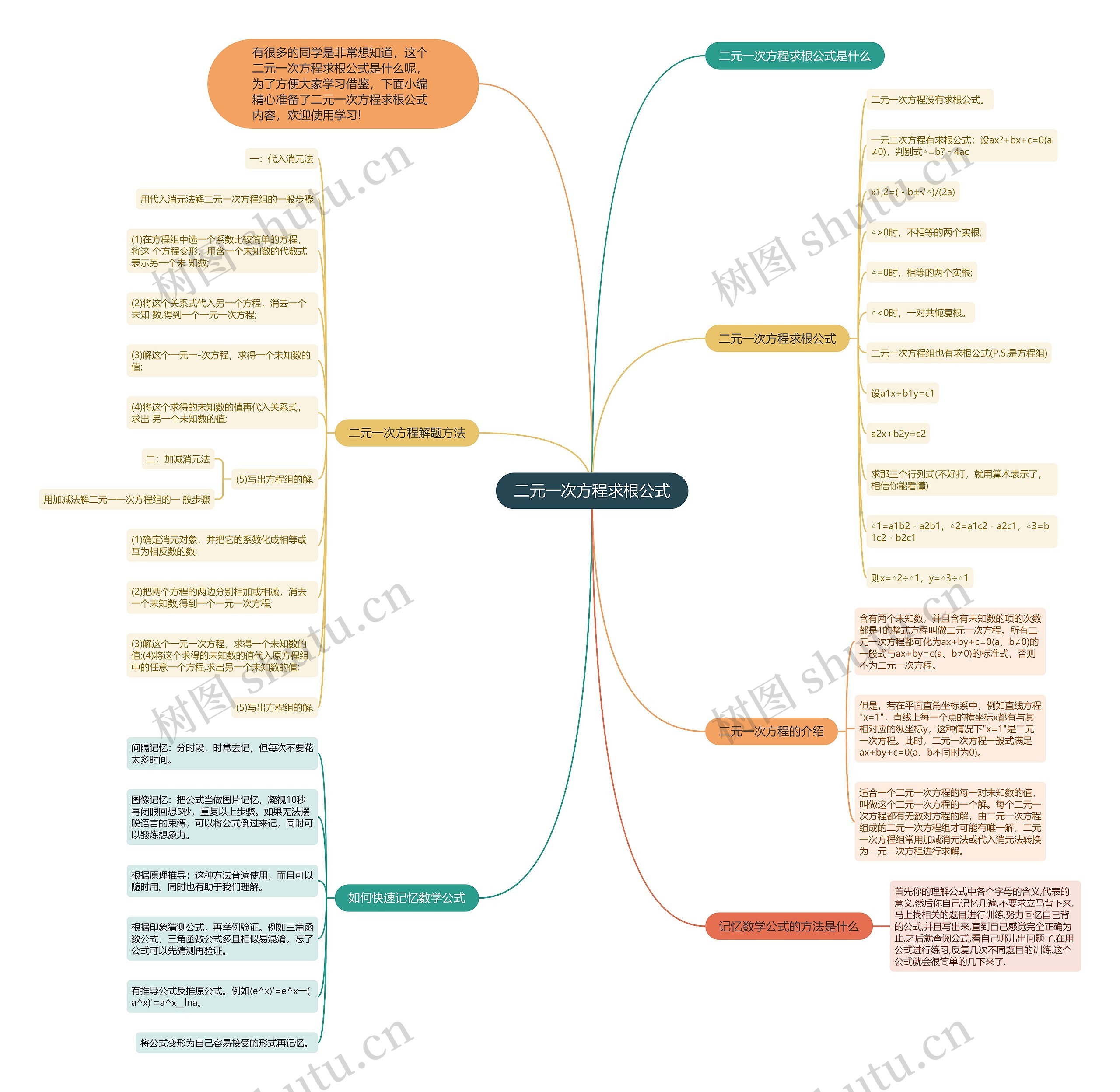
有很多的同学是非常想知道,这个二元一次方程求根公式是什么呢,为了方便大家学习借鉴,下面小编精心准备了二元一次方程求根公式内容,欢迎使用学习!
二元一次方程求根公式
二元一次方程没有求根公式。
一元二次方程有求根公式:设ax?+bx+c=0(a≠0),判别式△=b?﹣4ac
x1,2=(﹣b±√△)/(2a)
△>0时,不相等的两个实根;
△=0时,相等的两个实根;
△<0时,一对共轭复根。
二元一次方程组也有求根公式(P.S.是方程组)
设a1x+b1y=c1
a2x+b2y=c2
求那三个行列式(不好打,就用算术表示了,相信你能看懂)
△1=a1b2﹣a2b1,△2=a1c2﹣a2c1,△3=b1c2﹣b2c1
则x=△2÷△1,y=△3÷△1
二元一次方程解题方法
一:代入消元法
用代入消元法解二元一次方程组的一般步骤
(1)在方程组中选一个系数比较简单的方程,将这 个方程变形,用含一个未知数的代数式表示另一个未 知数;
(2)将这个关系式代入另一个方程,消去一个未知 数,得到一个一元一次方程;
(3)解这个一元一-次方程,求得一个未知数的值;
(4)将这个求得的未知数的值再代入关系式,求出 另一个未知数的值;
(5)写出方程组的解.
二:加减消元法
用加减法解二元一一次方程组的一 般步骤
(1)确定消元对象,并把它的系数化成相等或互为相反数的数;
(2)把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;
(3)解这个一元一次方程,求得一个未知数的值;(4)将这个求得的未知数的值代入原方程组中的任意一个方程,求出另一个未知数的值;
(5)写出方程组的解.
二元一次方程的介绍
含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。所有二元一次方程都可化为ax+by+c=0(a、b≠0)的一般式与ax+by=c(a、b≠0)的标准式,否则不为二元一次方程。
但是,若在平面直角坐标系中,例如直线方程"x=1",直线上每一个点的横坐标x都有与其相对应的纵坐标y,这种情况下"x=1"是二元一次方程。此时,二元一次方程一般式满足ax+by+c=0(a、b不同时为0)。
适合一个二元一次方程的每一对未知数的值,叫做这个二元一次方程的一个解。每个二元一次方程都有无数对方程的解,由二元一次方程组成的二元一次方程组才可能有唯一解,二元一次方程组常用加减消元法或代入消元法转换为一元一次方程进行求解。
如何快速记忆数学公式
间隔记忆:分时段,时常去记,但每次不要花太多时间。
图像记忆:把公式当做图片记忆,凝视10秒再闭眼回想5秒,重复以上步骤。如果无法摆脱语言的束缚,可以将公式倒过来记,同时可以锻炼想象力。
根据原理推导:这种方法普遍使用,而且可以随时用。同时也有助于我们理解。
根据印象猜测公式,再举例验证。例如三角函数公式,三角函数公式多且相似易混淆,忘了公式可以先猜测再验证。
有推导公式反推原公式。例如(e^x)'=e^x→(a^x)'=a^x__lna。
将公式变形为自己容易接受的形式再记忆。
记忆数学公式的方法是什么
首先你的理解公式中各个字母的含义,代表的意义.然后你自己记忆几遍,不要求立马背下来.马上找相关的题目进行训练,努力回忆自己背的公式,并且写出来,直到自己感觉完全正确为止,之后就查阅公式,看自己哪儿出问题了,在用公式进行练习,反复几次不同题目的训练,这个公式就会很简单的几下来了.
相关思维导图模板
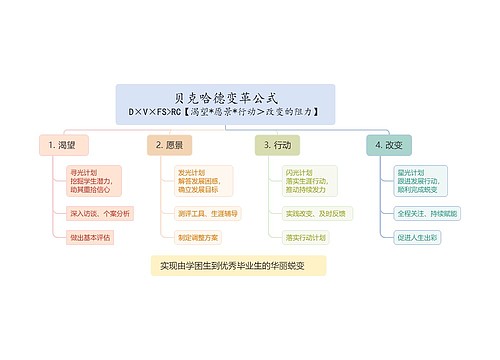

树图思维导图提供 贝克哈德变革公式D×V×FS>RC【渴望*愿景*行动>改变的阻力】 在线思维导图免费制作,点击“编辑”按钮,可对 贝克哈德变革公式D×V×FS>RC【渴望*愿景*行动>改变的阻力】 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1aa461813e5322a2460bc11ee9ac0afc
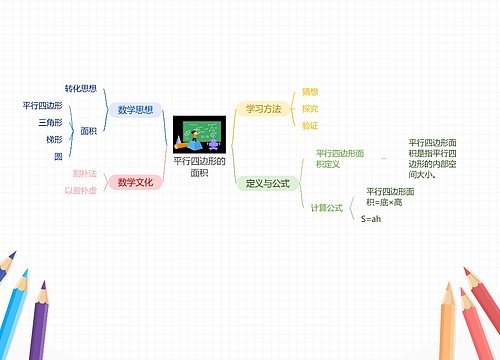

树图思维导图提供 平行四边形的面积 在线思维导图免费制作,点击“编辑”按钮,可对 平行四边形的面积 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:2063e4017045caf3585d5f7d4dfc6461














 上海工商
上海工商