周长怎么算直径圆的相关公式思维导图
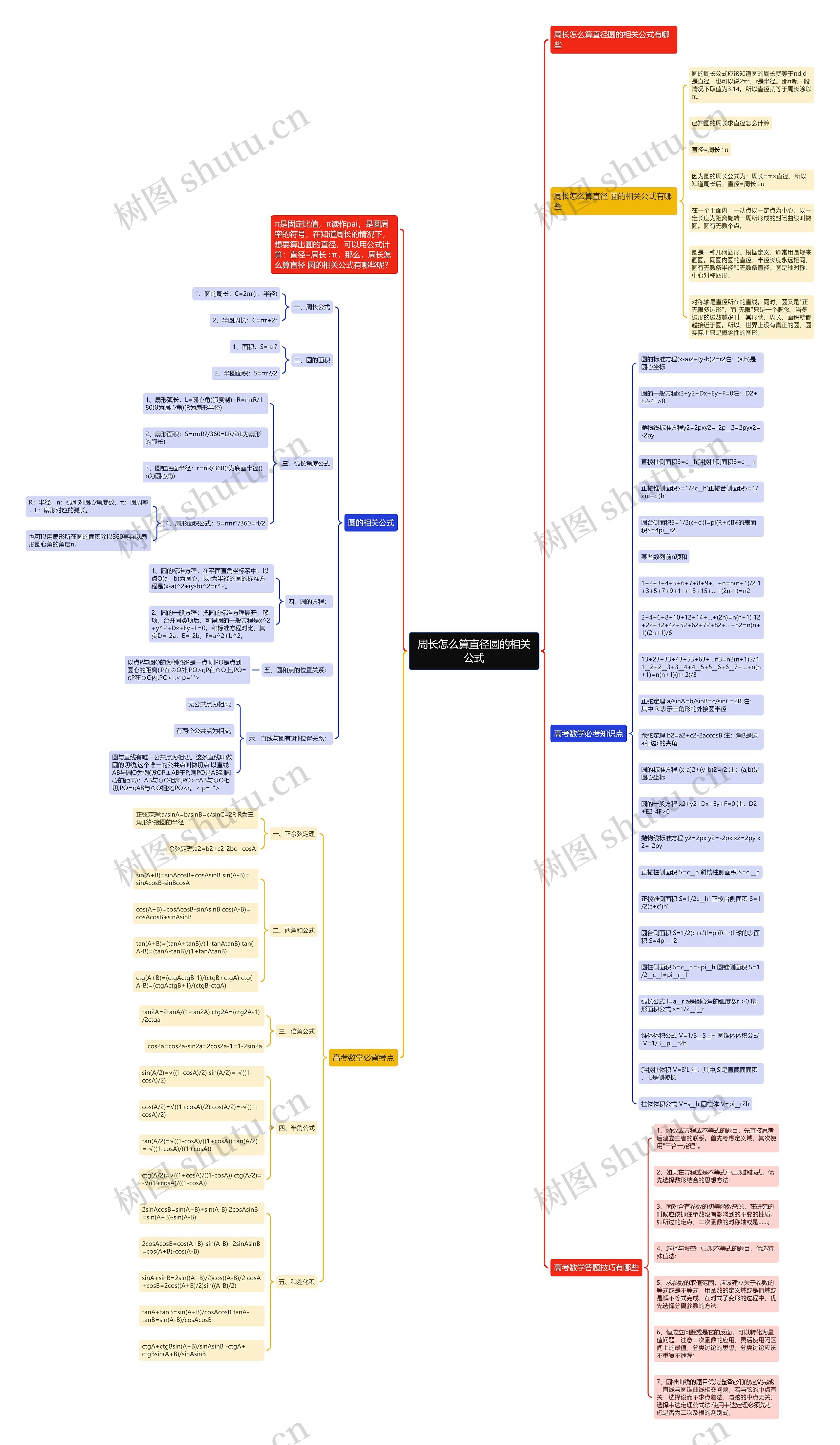
π是固定比值,π读作pai,是圆周率的符号,在知道周长的情况下,想要算出圆的直径,可以用公式计算:直径=周长÷π,那么,周长怎么算直径 圆的相关公式有哪些呢?周长怎么算直径 圆的相关公式有哪些圆的周长
树图思维导图提供 周长怎么算直径圆的相关公式 在线思维导图免费制作,点击“编辑”按钮,可对 周长怎么算直径圆的相关公式 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10d2f0400a4d580ac6fc1b4a2dd2d379
思维导图大纲
周长怎么算直径圆的相关公式思维导图模板大纲
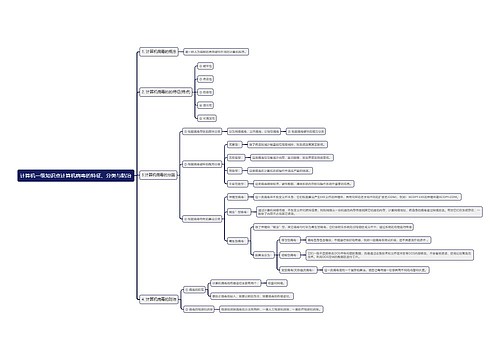
周长怎么算直径圆的相关公式有哪些
π是固定比值,π读作pai,是圆周率的符号,在知道周长的情况下,想要算出圆的直径,可以用公式计算:直径=周长÷π,那么,周长怎么算直径 圆的相关公式有哪些呢?
周长怎么算直径 圆的相关公式有哪些
圆的周长公式应该知道圆的周长就等于πd,d是直径,也可以说2πr,r是半径。那π呢一般情况下取值为3.14。所以直径就等于周长除以π。
已知圆的周长求直径怎么计算
直径=周长÷π
因为圆的周长公式为:周长=π×直径,所以知道周长后,直径=周长÷π
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。圆有无数个点。
圆是一种几何图形。根据定义,通常用圆规来画圆。同圆内圆的直径、半径长度永远相同,圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。
对称轴是直径所在的直线。同时,圆又是"正无限多边形",而"无限"只是一个概念。当多边形的边数越多时,其形状、周长、面积就都越接近于圆。所以,世界上没有真正的圆,圆实际上只是概念性的图形。
圆的相关公式
一、周长公式
1、圆的周长:C=2πr(r:半径)
2、半圆周长:C=πr+2r
二、圆的面积
1、面积:S=πr?
2、半圆面积:S=πr?/2
三、弧长角度公式
1、扇形弧长:L=圆心角(弧度制)×R=nπR/180(θ为圆心角)(R为扇形半径)
2、扇形面积:S=nπR?/360=LR/2(L为扇形的弧长)
3、圆锥底面半径:r=nR/360(r为底面半径)(n为圆心角)
4、扇形面积公式:S=nπr?/360=rl/2
R:半径,n:弧所对圆心角度数,π:圆周率,L:扇形对应的弧长。
也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n。
四、圆的方程:
1、圆的标准方程:在平面直角坐标系中,以点O(a,b)为圆心,以r为半径的圆的标准方程是(x-a)^2+(y-b)^2=r^2。
2、圆的一般方程:把圆的标准方程展开,移项,合并同类项后,可得圆的一般方程是x^2+y^2+Dx+Ey+F=0。和标准方程对比,其实D=-2a,E=-2b,F=a^2+b^2。
五、圆和点的位置关系:
以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r.< p="">
六、直线与圆有3种位置关系:
无公共点为相离;
有两个公共点为相交;
圆与直线有唯一公共点为相切。这条直线叫做圆的切线,这个唯一的公共点叫做切点.以直线AB与圆O为例(设OP⊥AB于P,则PO是AB到圆心的距离):AB与⊙O相离,PO>r;AB与⊙O相切,PO=r;AB与⊙O相交,PO<r。< p="">
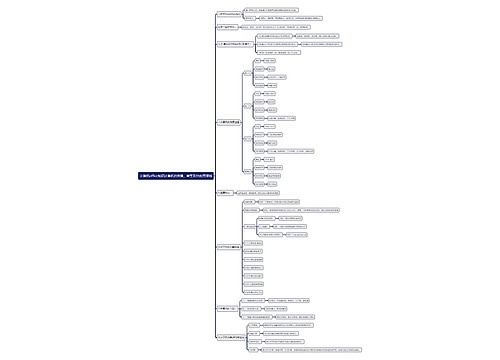
高考数学必考知识点
圆的标准方程(x-a)2+(y-b)2=r2注:(a,b)是圆心坐标
圆的一般方程x2+y2+Dx+Ey+F=0注:D2+E2-4F>0
抛物线标准方程y2=2pxy2=-2p__2=2pyx2=-2py
直棱柱侧面积S=c__h斜棱柱侧面积S=c'__h
正棱锥侧面积S=1/2c__h'正棱台侧面积S=1/2(c+c')h'
圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi__r2
某些数列前n项和
1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n2
2+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6
13+23+33+43+53+63+…n3=n2(n+1)2/4 1__2+2__3+3__4+4__5+5__6+6__7+…+n(n+1)=n(n+1)(n+2)/3
正弦定理 a/sinA=b/sinB=c/sinC=2R 注: 其中 R 表示三角形的外接圆半径
余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角
圆的标准方程 (x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标
圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0
抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py
直棱柱侧面积 S=c__h 斜棱柱侧面积 S=c'__h
正棱锥侧面积 S=1/2c__h' 正棱台侧面积 S=1/2(c+c')h'
圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi__r2
圆柱侧面积 S=c__h=2pi__h 圆锥侧面积 S=1/2__c__l=pi__r__l
弧长公式 l=a__r a是圆心角的弧度数r >0 扇形面积公式 s=1/2__l__r
锥体体积公式 V=1/3__S__H 圆锥体体积公式 V=1/3__pi__r2h
斜棱柱体积 V=S'L 注:其中,S'是直截面面积, L是侧棱长
柱体体积公式 V=s__h 圆柱体 V=pi__r2h
高考数学必背考点
一、正余弦定理
正弦定理:a/sinA=b/sinB=c/sinC=2R R为三角形外接圆的半径
余弦定理:a2=b2+c2-2bc__cosA
二、两角和公式
sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA
cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)
ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)
三、倍角公式
tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga
cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a
四、半角公式
sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)
cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)
tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))
ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))
五、和差化积
2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)
2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)
sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2)
tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB
ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB
高考数学答题技巧有哪些
1、函数或方程或不等式的题目,先直接思考后建立三者的联系。首先考虑定义域,其次使用"三合一定理"。
2、如果在方程或是不等式中出现超越式,优先选择数形结合的思想方法;
3、面对含有参数的初等函数来说,在研究的时候应该抓住参数没有影响到的不变的性质。如所过的定点,二次函数的对称轴或是……;
4、选择与填空中出现不等式的题目,优选特殊值法;
5、求参数的取值范围,应该建立关于参数的等式或是不等式,用函数的定义域或是值域或是解不等式完成,在对式子变形的过程中,优先选择分离参数的方法;
6、恒成立问题或是它的反面,可以转化为最值问题,注意二次函数的应用,灵活使用闭区间上的最值,分类讨论的思想,分类讨论应该不重复不遗漏;
7、圆锥曲线的题目优先选择它们的定义完成,直线与圆锥曲线相交问题,若与弦的中点有关,选择设而不求点差法,与弦的中点无关,选择韦达定理公式法;使用韦达定理必须先考虑是否为二次及根的判别式。
相关思维导图模板


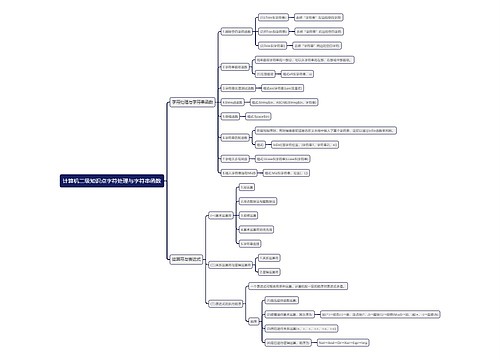
树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 影子还可以怎么玩 在线思维导图免费制作,点击“编辑”按钮,可对 影子还可以怎么玩 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4d614e09bfb803c46b43c88c3b44bc79





 上海工商
上海工商