人教版高一上册数学知识点总结思维导图

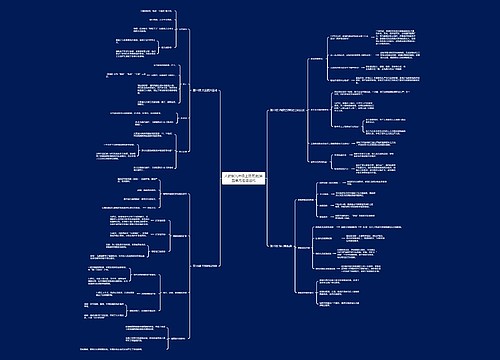
人教版高一上册数学知识点总结思维导图涵盖多个关键知识点,函数的定义包含自变量、函数值、对应关系、定义域和值域,函数的定义域需要符合一定条件,构成函数的三要素是定义域、对应关系和值域,而函数的相等需要满足定义域和对应关系完全一致的条件。第三,函数的图象是以自变量和函数值为坐标的点的集合,通常是光滑的连续曲线或直线。绘制函数图象的方法有描点法和常用变换方法,可以通过数形结合的方法分析解题的思路,这些知识点是学习人教版高一上册数学的基础,对于学生掌握数学知识和解题有重要的帮助。
思维导图大纲
人教版高一上册数学知识点总结思维导图模板大纲
【篇一】
1.函数的概念:设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有确定的数fx和它对应,那么就称f:A→B为从集合A到集合B的一个函数.记作:y=fx,x∈A.其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合fx|x∈A叫做函数的值域.
注意:2如果只给出解析式y=fx,而没有指明它的定义域,则函数的定义域即是指能使这个式子有意义的实数的集合;3函数的定义域、值域要写成集合或区间的形式.
定义域补充
能使函数式有意义的实数x的集合称为函数的定义域,求函数的定义域时列不等式组的主要依据是:1分式的分母不等于零;2偶次方根的被开方数不小于零;3对数式的真数必须大于零;4指数、对数式的底必须大于零且不等于1.5如果函数是由一些基本函数通过四则运算结合而成的.那么,它的定义域是使各部分都有意义的x的值组成的集合.6指数为零底不可以等于零6实际问题中的函数的定义域还要保证实际问题有意义.
构成函数的三要素:定义域、对应关系和值域
再注意:1构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全一致,即称这两个函数相等或为同一函数2两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关。相同函数的判断方法:①表达式相同;②定义域一致两点必须同时具备
值域补充
1、函数的值域取决于定义域和对应法则,不论采取什么方法求函数的值域都应先考虑其定义域.2.应熟悉掌握一次函数、二次函数、指数、对数函数及各三角函数的值域,它是求解复杂函数值域的基础。
3.函数图象知识归纳
1定义:在平面直角坐标系中,以函数y=fx,x∈A中的x为横坐标,函数值y为纵坐标的点Px,y的集合C,叫做函数y=fx,x∈A的图象.
C上每一点的坐标x,y均满足函数关系y=fx,反过来,以满足y=fx的每一组有序实数对x、y为坐标的点x,y,均在C上.即记为C=Px,y|y=fx,x∈A
图象C一般的是一条光滑的连续曲线或直线,也可能是由与任意平行与Y轴的直线最多只有一个交点的若干条曲线或离散点组成。
2画法
A、描点法:根据函数解析式和定义域,求出x,y的一些对应值并列表,以x,y为坐标在坐标系内描出相应的点Px,y,最后用平滑的曲线将这些点连接起来.
B、图象变换法请参考必修4三角函数
常用变换方法有三种,即平移变换、伸缩变换和对称变换
3作用:
1、直观的看出函数的性质;2、利用数形结合的方法分析解题的思路。提高解题的速度。
【篇二】
一、集合有关概念
1、集合的含义:某些指定的对象集在一起就成为一个集合,其中每一个对象叫元素。
2、集合的中元素的三个特性:
1.元素的确定性;2.元素的互异性;3.元素的无序性
说明:1对于一个给定的集合,集合中的元素是确定的,任何一个对象或者是或者不是这个给定的集合的元素。
2任何一个给定的集合中,任何两个元素都是不同的对象,相同的对象归入一个集合时,仅算一个元素。
3集合中的元素是平等的,没有先后顺序,因此判定两个集合是否一样,仅需比较它们的元素是否一样,不需考查排列顺序是否一样。
4集合元素的三个特性使集合本身具有了确定性和整体性。
3、集合的表示:…如我校的篮球队员,太平洋,大西洋,印度洋,北冰洋
1.用拉丁字母表示集合:A=我校的篮球队员,B=1,2,3,4,5
2.集合的表示方法:列举法与描述法。
二、集合间的基本关系
1.“包含”关系—子集
注意:有两种可能1A是B的一部分,;2A与B是同一集合。
反之:集合A不包含于集合B,或集合B不包含集合A,记作AB或BA
2.“相等”关系5≥5,且5≤5,则5=5
实例:设A=x|x2-1=0B=-1,1“元素相同”
结论:对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时,集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,即:A=B
①任何一个集合是它本身的子集。AíA
②真子集:如果AíB,且A1B那就说集合A是集合B的真子集,记作AB或BA
③如果AíB,BíC,那么AíC
④如果AíB同时BíA那么A=B
3.不含任何元素的集合叫做空集,记为Φ
规定:空集是任何集合的子集,空集是任何非空集合的真子集。
三、集合的运算
1.交集的定义:一般地,由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.
记作A∩B读作”A交B”,即A∩B=x|x∈A,且x∈B.
2、并集的定义:一般地,由所有属于集合A或属于集合B的元素所组成的集合,叫做A,B的并集。记作:A∪B读作”A并B”,即A∪B=x|x∈A,或x∈B.
3、交集与并集的性质:A∩A=A,A∩φ=φ,A∩B=B∩A,A∪A=A,A∪φ=A,A∪B=B∪A.
相关思维导图模板
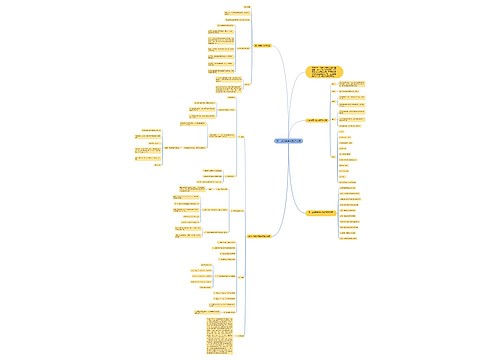

树图思维导图提供 高一上册数学知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 高一上册数学知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:cbbdd4ae8a4e3ef541c83a7665121ee8
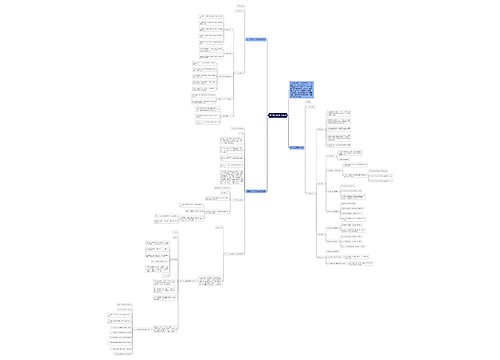

树图思维导图提供 初二数学知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 初二数学知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9a7b26fb70bd13f48ab013e90f31b276









 上海工商
上海工商