高三下册数学知识点归纳思维导图

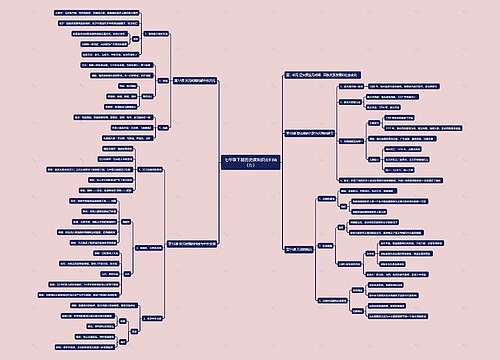
高三下册数学知识点归纳思维导图,包含导数的第一定义、第二定义、导函数和导数的求法,多项式函数单调性的利用导数研究和求解单调区间的方法,排列和组合的定义,和排列数和组合数的公式和性质。其中导数是函数学习的重点,包含导数的定义和求法,和导函数的概念,而单调性则是其应用,可以通过导数来研究函数单调性和求解单调区间,排列和组合是概率学习中的基础概念,需要了解其定义和相应的公式和性质。
思维导图大纲
高三下册数学知识点归纳思维导图模板大纲
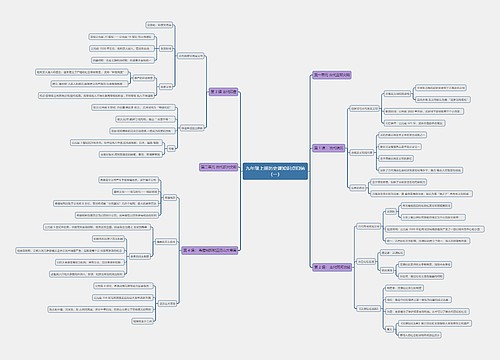
【篇一】高三下册数学知识点归纳
设函数y=fx在点x0的某个领域内有定义,当自变量x在x0处有增量△xx0+△x也在该邻域内时,相应地函数取得增量△y=fx0+△x-fx0;如果△y与△x之比当△x→0时极限存在,则称函数y=fx在点x0处可导,并称这个极限值为函数y=fx在点x0处的导数记为f'x0,即导数第一定义
二导数第二定义
设函数y=fx在点x0的某个领域内有定义,当自变量x在x0处有变化△xx-x0也在该邻域内时,相应地函数变化△y=fx-fx0;如果△y与△x之比当△x→0时极限存在,则称函数y=fx在点x0处可导,并称这个极限值为函数y=fx在点x0处的导数记为f'x0,即导数第二定义
三导函数与导数
如果函数y=fx在开区间I内每一点都可导,就称函数fx在区间I内可导。这时函数y=fx对于区间I内的每一个确定的x值,都对应着一个确定的导数,这就构成一个新的函数,称这个函数为原来函数y=fx的导函数,记作y',f'x,dy/dx,dfx/dx。导函数简称导数。
四单调性及其应用
1.利用导数研究多项式函数单调性的一般步骤
1求f¢x
2确定f¢x在a,b内符号3若f¢x>0在a,b上恒成立,则fx在a,b上是增函数;若f¢x<0在a,b上恒成立,则fx在a,b上是减函数
2.用导数求多项式函数单调区间的一般步骤
1求f¢x
2f¢x>0的解集与定义域的交集的对应区间为增区间;f¢x<0的解集与定义域的交集的对应区间为减区间
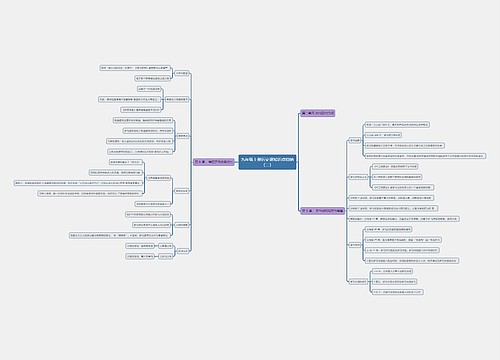
【篇二】高三下册数学知识点归纳
一、排列
1定义
1从n个不同元素中取出m个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一排列。
2从n个不同元素中取出m个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,记为Amn.
2排列数的公式与性质
1排列数的公式:Amn=nn-1n-2…n-m+1
特例:当m=n时,Amn=n!=nn-1n-2…×3×2×1
规定:0!=1
二、组合
1定义
1从n个不同元素中取出m个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合
2从n个不同元素中取出m个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号Cmn表示。
2比较与鉴别
由排列与组合的定义知,获得一个排列需要“取出元素”和“对取出元素按一定顺序排成一列”两个过程,而获得一个组合只需要“取出元素”,不管怎样的顺序并成一组这一个步骤。
排列与组合的区别在于组合仅与选取的元素有关,而排列不仅与选取的元素有关,而且还与取出元素的顺序有关。因此,所给问题是否与取出元素的顺序有关,是判断这一问题是排列问题还是组合问题的理论依据。
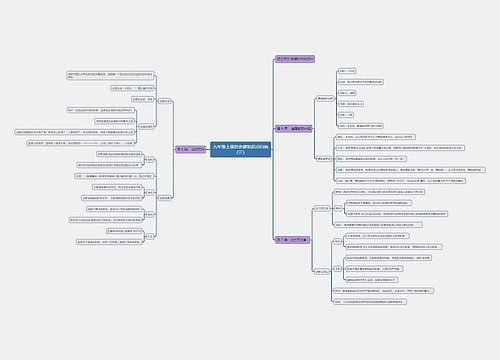
三、排列组合与二项式定理知识点
1.计数原理知识点
①乘法原理:N=n1·n2·n3·…nM分步②加法原理:N=n1+n2+n3+…+nM分类
2.排列有序与组合无序
Anm=nn-1n-2n-3-…n-m+1=n!/n-m!Ann=n!
Cnm=n!/n-m!m!
Cnm=Cnn-mCnm+Cnm+1=Cn+1m+1k•k!=k+1!-k!
3.排列组合混合题的解题原则:先选后排,先分再排
排列组合题的主要解题方法:优先法:以元素为主,应先满足特殊元素的要求,再考虑其他元素.以位置为主考虑,即先满足特殊位置的要求,再考虑其他位置.
捆绑法集团元素法,把某些必须在一起的元素视为一个整体考虑
插空法解决相间问题间接法和去杂法等等
在求解排列与组合应用问题时,应注意:
1把具体问题转化或归结为排列或组合问题;
2通过分析确定运用分类计数原理还是分步计数原理;
3分析题目条件,避免“选取”时重复和遗漏;
4列出式子计算和作答.
经常运用的数学思想是:
①分类讨论思想;②转化思想;③对称思想.
4.二项式定理知识点:
①a+bn=Cn0ax+Cn1an-1b1+Cn2an-2b2+Cn3an-3b3+…+Cnran-rbr+-…+Cnn-1abn-1+Cnnbn
特别地:1+xn=1+Cn1x+Cn2x2+…+Cnrxr+…+Cnnxn
②主要性质和主要结论:对称性Cnm=Cnn-m
二项式系数在中间。要注意n为奇数还是偶数,答案是中间一项还是中间两项
所有二项式系数的和:Cn0+Cn1+Cn2+Cn3+Cn4+…+Cnr+…+Cnn=2n
奇数项二项式系数的和=偶数项而是系数的和
Cn0+Cn2+Cn4+Cn6+Cn8+…=Cn1+Cn3+Cn5+Cn7+Cn9+…=2n-1
③通项为第r+1项:Tr+1=Cnran-rbr作用:处理与指定项、特定项、常数项、有理项等有关问题。
5.二项式定理的应用:解决有关近似计算、整除问题,运用二项展开式定理并且结合放缩法证明与指数有关的不等式。
6.注意二项式系数与项的系数字母项的系数,指定项的系数等,指运算结果的系数的区别,在求某几项的系数的和时注意赋值法的应用。
相关思维导图模板

树图思维导图提供 高考数学重点知识点2021 在线思维导图免费制作,点击“编辑”按钮,可对 高考数学重点知识点2021 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:684a1d1c5217c63d1bf43d672e4e5488


树图思维导图提供 高考考前必看数学知识点 在线思维导图免费制作,点击“编辑”按钮,可对 高考考前必看数学知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ce2d1cf3f7311563759aaabda1e4c05a







 上海工商
上海工商