高一年级数学必修三知识点总结思维导图
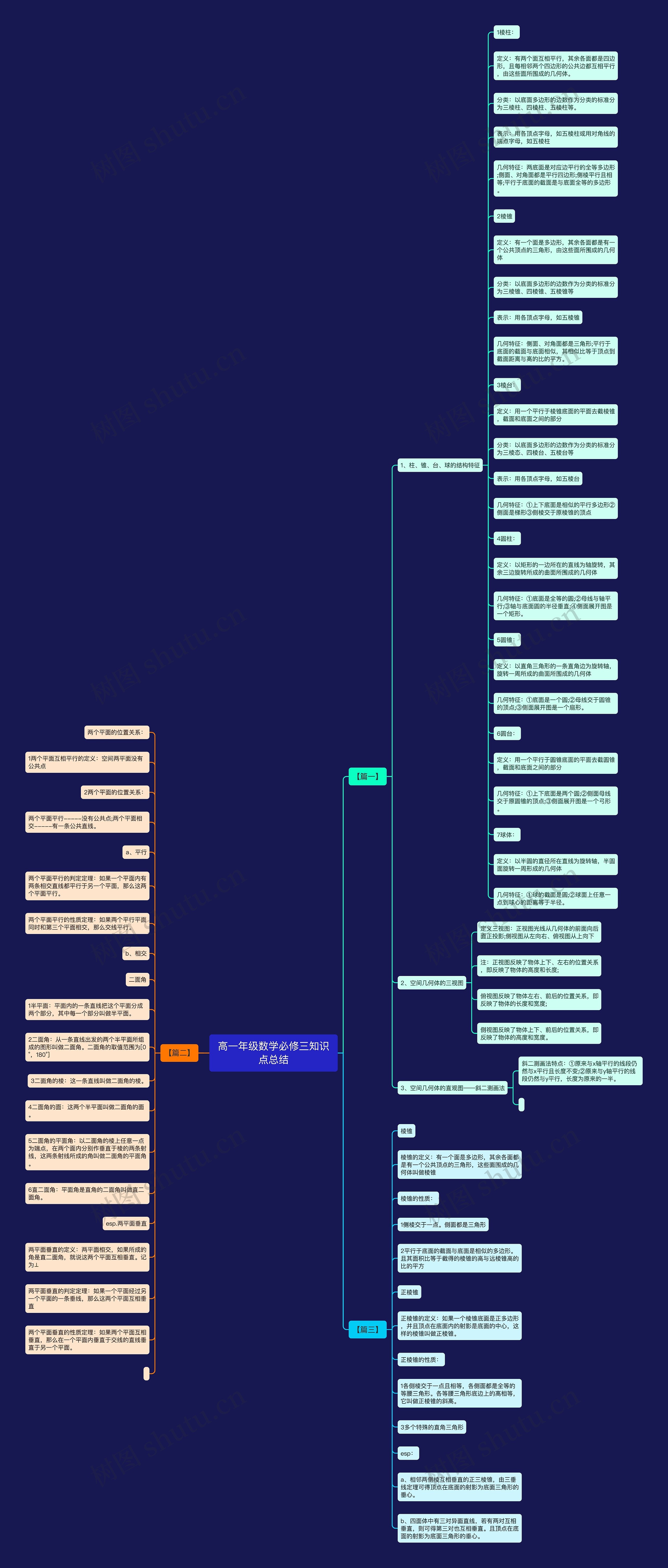
高一年级数学必修三知识点总结思维导图,具体内容包含空间几何体的结构特征、三视图和斜二测画法,空间几何体包含柱、锥、台和球,并详细介绍了各自的定义、分类、表示和几何特征,而三视图则是指空间几何体在不同视角下的展现方式,包含正视图、侧视图和俯视图。而斜二测画法则是一种直观的绘画方式,通过保持线段与坐标轴平行且长度比例不变的特点,将空间几何体以更加真实的形式呈现出来。
思维导图大纲
高一年级数学必修三知识点总结思维导图模板大纲
【篇一】
1、柱、锥、台、球的结构特征
1棱柱:
定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱或用对角线的端点字母,如五棱柱
几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
2棱锥
定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体
分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等
表示:用各顶点字母,如五棱锥
几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
3棱台:
定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分
分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等
表示:用各顶点字母,如五棱台
几何特征:①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点
4圆柱:
定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体
几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
5圆锥:
定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体
几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
6圆台:
定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分
几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
7球体:
定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体
几何特征:①球的截面是圆;②球面上任意一点到球心的距离等于半径。
2、空间几何体的三视图
定义三视图:正视图光线从几何体的前面向后面正投影;侧视图从左向右、俯视图从上向下
注:正视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;
俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;
侧视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度。
3、空间几何体的直观图——斜二测画法
斜二测画法特点:①原来与x轴平行的线段仍然与x平行且长度不变;②原来与y轴平行的线段仍然与y平行,长度为原来的一半。
【篇二】
两个平面的位置关系:
1两个平面互相平行的定义:空间两平面没有公共点
2两个平面的位置关系:
两个平面平行-----没有公共点;两个平面相交-----有一条公共直线。
a、平行
两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么交线平行。
b、相交
二面角
1半平面:平面内的一条直线把这个平面分成两个部分,其中每一个部分叫做半平面。
2二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。二面角的取值范围为[0°,180°]
3二面角的棱:这一条直线叫做二面角的棱。
4二面角的面:这两个半平面叫做二面角的面。
5二面角的平面角:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
6直二面角:平面角是直角的二面角叫做直二面角。
esp.两平面垂直
两平面垂直的定义:两平面相交,如果所成的角是直二面角,就说这两个平面互相垂直。记为⊥
两平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直
两个平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于交线的直线垂直于另一个平面。
【篇三】
棱锥
棱锥的定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,这些面围成的几何体叫做棱锥
棱锥的性质:
1侧棱交于一点。侧面都是三角形
2平行于底面的截面与底面是相似的多边形。且其面积比等于截得的棱锥的高与远棱锥高的比的平方
正棱锥
正棱锥的定义:如果一个棱锥底面是正多边形,并且顶点在底面内的射影是底面的中心,这样的棱锥叫做正棱锥。
正棱锥的性质:
1各侧棱交于一点且相等,各侧面都是全等的等腰三角形。各等腰三角形底边上的高相等,它叫做正棱锥的斜高。
3多个特殊的直角三角形
esp:
a、相邻两侧棱互相垂直的正三棱锥,由三垂线定理可得顶点在底面的射影为底面三角形的垂心。
b、四面体中有三对异面直线,若有两对互相垂直,则可得第三对也互相垂直。且顶点在底面的射影为底面三角形的垂心。
相关思维导图模板


树图思维导图提供 高一必修一数学知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 高一必修一数学知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ceeb060c56ea87ac16dbffe196536338


树图思维导图提供 高中数学必修三知识点归纳 在线思维导图免费制作,点击“编辑”按钮,可对 高中数学必修三知识点归纳 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:8dd66ac3c1628ff55d62cf296f96a40c



















 上海工商
上海工商