一元二次方程思维导图
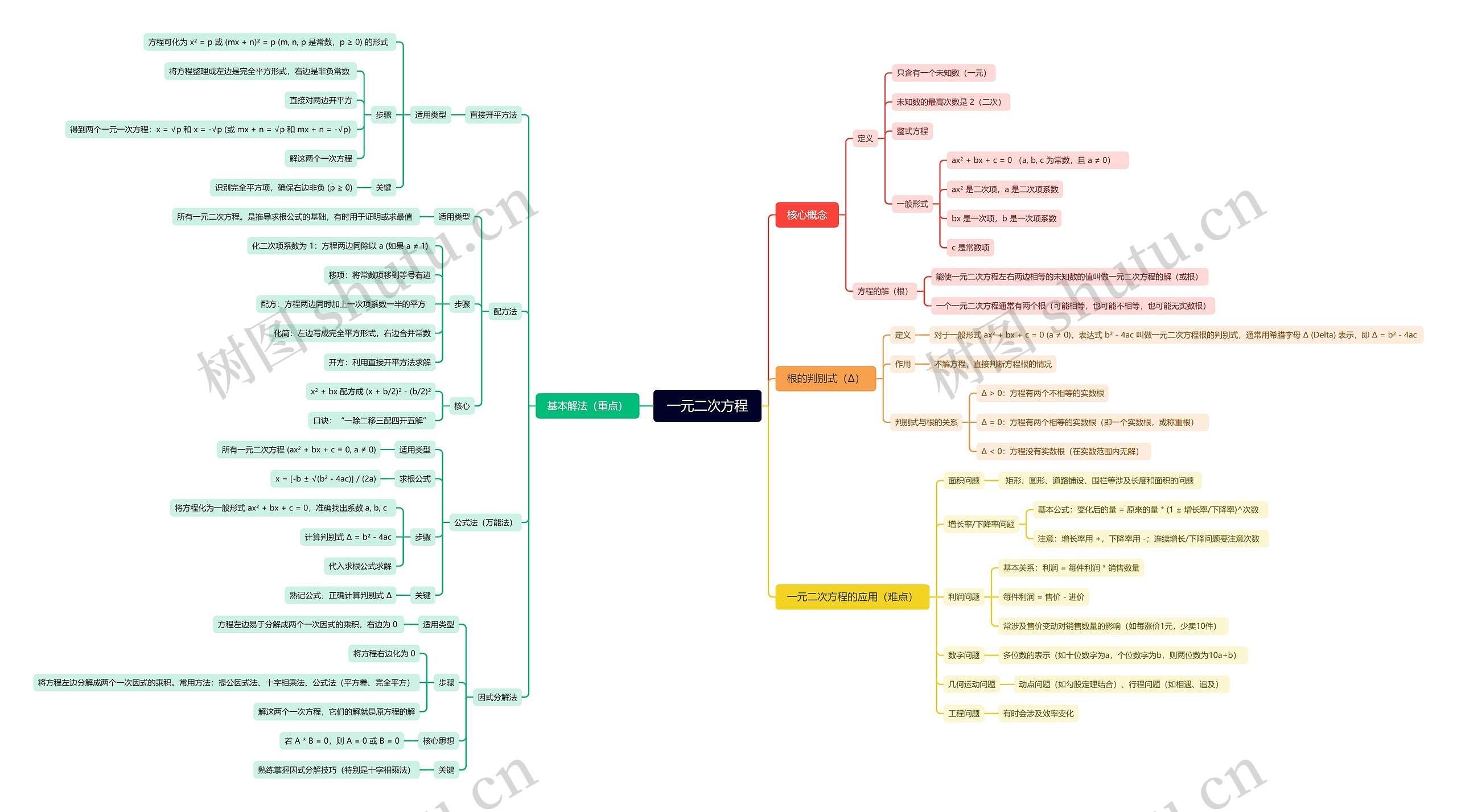
基本解法，核心概念相关内容讲解
树图思维导图提供 一元二次方程 在线思维导图免费制作，点击“编辑”按钮，可对 一元二次方程 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：4ea6786652a11e63eea8154e13b6549a
思维导图大纲
一元二次方程思维导图模板大纲
核心概念
定义
只含有一个未知数（一元）
未知数的最高次数是 2（二次）
整式方程
一般形式
ax² + bx + c = 0 （a, b, c 为常数，且 a ≠ 0）
ax² 是二次项，a 是二次项系数
bx 是一次项，b 是一次项系数
c 是常数项
方程的解（根）
能使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解（或根）
一个一元二次方程通常有两个根（可能相等，也可能不相等，也可能无实数根）
基本解法（重点）
直接开平方法
适用类型
方程可化为 x² = p 或 (mx + n)² = p (m, n, p 是常数，p ≥ 0) 的形式
步骤
将方程整理成左边是完全平方形式，右边是非负常数
直接对两边开平方
得到两个一元一次方程：x = √p 和 x = -√p (或 mx + n = √p 和 mx + n = -√p)
解这两个一次方程
关键
识别完全平方项，确保右边非负 (p ≥ 0)
配方法
适用类型
所有一元二次方程。是推导求根公式的基础，有时用于证明或求最值
步骤
化二次项系数为 1：方程两边同除以 a (如果 a ≠ 1)
移项：将常数项移到等号右边
配方：方程两边同时加上一次项系数一半的平方
化简：左边写成完全平方形式，右边合并常数
开方：利用直接开平方法求解
核心
x² + bx 配方成 (x + b/2)² - (b/2)²
口诀：“一除二移三配四开五解”
公式法（万能法）
适用类型
所有一元二次方程 (ax² + bx + c = 0, a ≠ 0)
求根公式
x = [-b ± √(b² - 4ac)] / (2a)
步骤
将方程化为一般形式 ax² + bx + c = 0，准确找出系数 a, b, c
计算判别式 Δ = b² - 4ac
代入求根公式求解
关键
熟记公式，正确计算判别式 Δ
因式分解法
适用类型
方程左边易于分解成两个一次因式的乘积，右边为 0
步骤
将方程右边化为 0
将方程左边分解成两个一次因式的乘积。常用方法：提公因式法、十字相乘法、公式法（平方差、完全平方）
解这两个一次方程，它们的解就是原方程的解
核心思想
若 A * B = 0，则 A = 0 或 B = 0
关键
熟练掌握因式分解技巧（特别是十字相乘法）
根的判别式（Δ）
定义
对于一般形式 ax² + bx + c = 0 (a ≠ 0)，表达式 b² - 4ac 叫做一元二次方程根的判别式，通常用希腊字母 Δ (Delta) 表示，即 Δ = b² - 4ac
作用
不解方程，直接判断方程根的情况
判别式与根的关系
Δ > 0：方程有两个不相等的实数根
Δ = 0：方程有两个相等的实数根（即一个实数根，或称重根）
Δ < 0：方程没有实数根（在实数范围内无解）
一元二次方程的应用（难点）
面积问题
矩形、圆形、道路铺设、围栏等涉及长度和面积的问题
增长率/下降率问题
基本公式：变化后的量 = 原来的量 * (1 ± 增长率/下降率)^次数
注意：增长率用 +，下降率用 -；连续增长/下降问题要注意次数
利润问题
基本关系：利润 = 每件利润 * 销售数量
每件利润 = 售价 - 进价
常涉及售价变动对销售数量的影响（如每涨价1元，少卖10件）
数字问题
多位数的表示（如十位数字为a，个位数字为b，则两位数为10a+b）
几何运动问题
动点问题（如勾股定理结合）、行程问题（如相遇、追及）
工程问题
有时会涉及效率变化
相关思维导图模板
树图思维导图提供 一元线性回归从建模到应用的全过程 在线思维导图免费制作，点击“编辑”按钮，可对 一元线性回归从建模到应用的全过程 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：a116e35696a4e946bb7795635f4520b3
树图思维导图提供 一元二次方程教学思维导图 在线思维导图免费制作，点击“编辑”按钮，可对 一元二次方程教学思维导图 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：1c082077678da4cbf954425a4a4f7d1f
相关思维导图专辑
Copyright©2022-2025 树图网shutu.cn 版权所有|上海聚石塔网络科技有限公司|网站备案号：沪ICP备2021036420号-3|
沪公网安备 31011502019485号|
上海工商