二次根式思维导图
核心性质,核心概念,运算规则相关内容讲解
树图思维导图提供 二次根式 在线思维导图免费制作,点击“编辑”按钮,可对 二次根式 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:e15265b7ae46b805ea1c4eda5f42e170
思维导图大纲
二次根式思维导图模板大纲
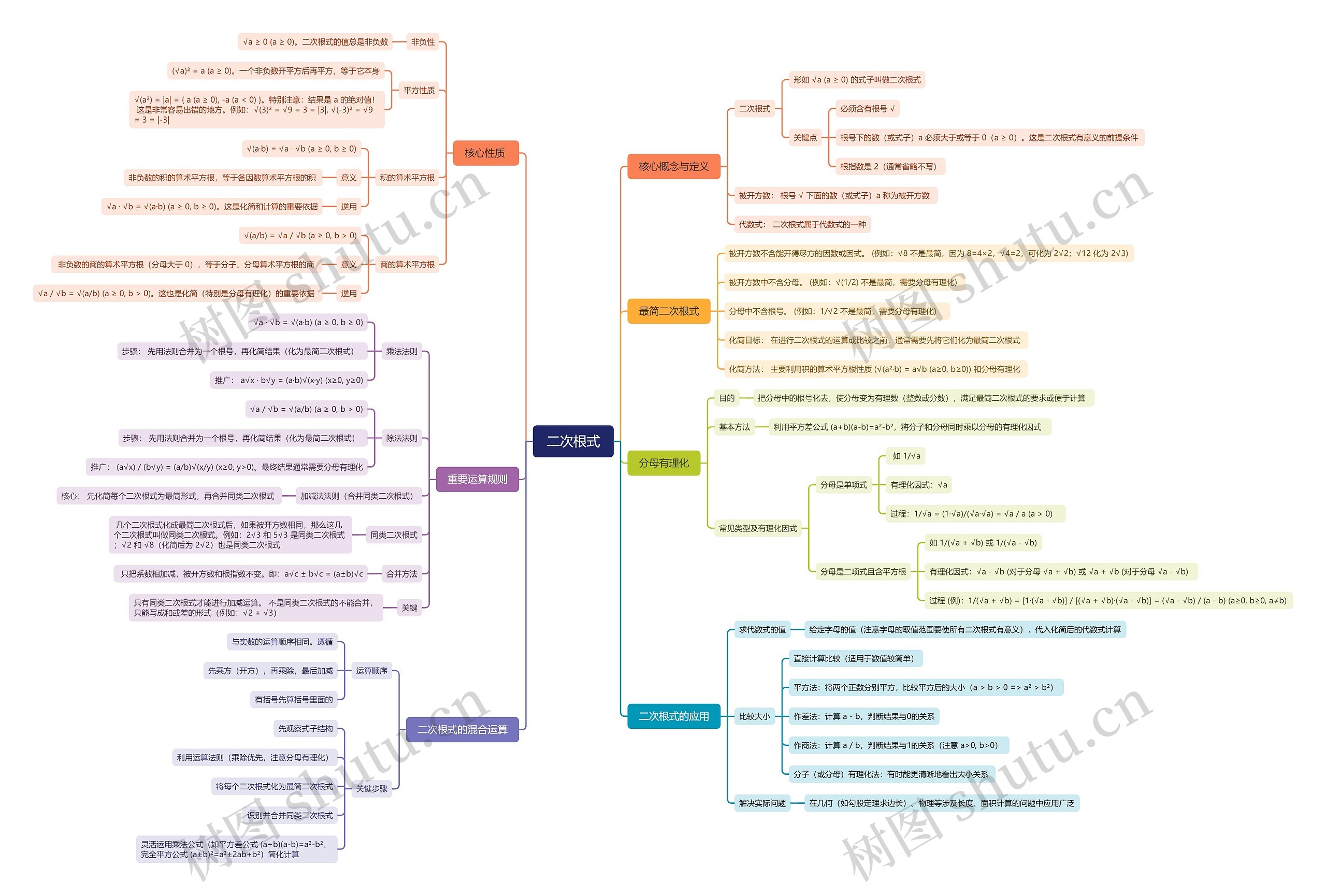
核心概念与定义
二次根式
形如 √a (a ≥ 0) 的式子叫做二次根式
关键点
必须含有根号 √
根号下的数(或式子)a 必须大于或等于 0(a ≥ 0)。这是二次根式有意义的前提条件
根指数是 2(通常省略不写)
被开方数: 根号 √ 下面的数(或式子)a 称为被开方数
代数式: 二次根式属于代数式的一种
核心性质
非负性
√a ≥ 0 (a ≥ 0)。二次根式的值总是非负数
平方性质
(√a)² = a (a ≥ 0)。一个非负数开平方后再平方,等于它本身
√(a²) = |a| = { a (a ≥ 0), -a (a < 0) }。特别注意:结果是 a 的绝对值! 这是非常容易出错的地方。例如:√(3)² = √9 = 3 = |3|, √(-3)² = √9 = 3 = |-3|
积的算术平方根
√(a·b) = √a · √b (a ≥ 0, b ≥ 0)
意义
非负数的积的算术平方根,等于各因数算术平方根的积
逆用
√a · √b = √(a·b) (a ≥ 0, b ≥ 0)。这是化简和计算的重要依据
商的算术平方根
√(a/b) = √a / √b (a ≥ 0, b > 0)
意义
非负数的商的算术平方根(分母大于 0),等于分子、分母算术平方根的商
逆用
√a / √b = √(a/b) (a ≥ 0, b > 0)。这也是化简(特别是分母有理化)的重要依据
重要运算规则
乘法法则
√a · √b = √(a·b) (a ≥ 0, b ≥ 0)
步骤: 先用法则合并为一个根号,再化简结果(化为最简二次根式)
推广: a√x · b√y = (a·b)√(x·y) (x≥0, y≥0)
除法法则
√a / √b = √(a/b) (a ≥ 0, b > 0)
步骤: 先用法则合并为一个根号,再化简结果(化为最简二次根式)
推广: (a√x) / (b√y) = (a/b)√(x/y) (x≥0, y>0)。最终结果通常需要分母有理化
加减法法则(合并同类二次根式)
核心: 先化简每个二次根式为最简形式,再合并同类二次根式
同类二次根式
几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式。例如:2√3 和 5√3 是同类二次根式;√2 和 √8(化简后为 2√2)也是同类二次根式
合并方法
只把系数相加减,被开方数和根指数不变。即:a√c ± b√c = (a±b)√c
关键
只有同类二次根式才能进行加减运算。 不是同类二次根式的不能合并,只能写成和或差的形式(例如:√2 + √3)
二次根式的混合运算
运算顺序
与实数的运算顺序相同。遵循
先乘方(开方),再乘除,最后加减
有括号先算括号里面的
关键步骤
先观察式子结构
利用运算法则(乘除优先,注意分母有理化)
将每个二次根式化为最简二次根式
识别并合并同类二次根式
灵活运用乘法公式(如平方差公式 (a+b)(a-b)=a²-b²、完全平方公式 (a±b)²=a²±2ab+b²)简化计算
最简二次根式
被开方数不含能开得尽方的因数或因式。 (例如:√8 不是最简,因为 8=4×2,√4=2,可化为 2√2;√12 化为 2√3)
被开方数中不含分母。 (例如:√(1/2) 不是最简,需要分母有理化)
分母中不含根号。 (例如:1/√2 不是最简,需要分母有理化)
化简目标: 在进行二次根式的运算或比较之前,通常需要先将它们化为最简二次根式
化简方法: 主要利用积的算术平方根性质 (√(a²·b) = a√b (a≥0, b≥0)) 和分母有理化
分母有理化
目的
把分母中的根号化去,使分母变为有理数(整数或分数),满足最简二次根式的要求或便于计算
基本方法
利用平方差公式 (a+b)(a-b)=a²-b²,将分子和分母同时乘以分母的有理化因式
常见类型及有理化因式
分母是单项式
如 1/√a
有理化因式:√a
过程:1/√a = (1·√a)/(√a·√a) = √a / a (a > 0)
分母是二项式且含平方根
如 1/(√a + √b) 或 1/(√a - √b)
有理化因式:√a - √b (对于分母 √a + √b) 或 √a + √b (对于分母 √a - √b)
过程 (例):1/(√a + √b) = [1·(√a - √b)] / [(√a + √b)·(√a - √b)] = (√a - √b) / (a - b) (a≥0, b≥0, a≠b)
二次根式的应用
求代数式的值
给定字母的值(注意字母的取值范围要使所有二次根式有意义),代入化简后的代数式计算
比较大小
直接计算比较(适用于数值较简单)
平方法:将两个正数分别平方,比较平方后的大小(a > b > 0 => a² > b²)
作差法:计算 a - b,判断结果与0的关系
作商法:计算 a / b,判断结果与1的关系(注意 a>0, b>0)
分子(或分母)有理化法:有时能更清晰地看出大小关系
解决实际问题
在几何(如勾股定理求边长)、物理等涉及长度、面积计算的问题中应用广泛
相关思维导图模板

树图思维导图提供 在党的二十届三中全会第二次全体会议上的讲话 在线思维导图免费制作,点击“编辑”按钮,可对 在党的二十届三中全会第二次全体会议上的讲话 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:3f87b3e9597430e443dcb980efa0ea2d


树图思维导图提供 3#工程建模思路 在线思维导图免费制作,点击“编辑”按钮,可对 3#工程建模思路 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:449f50705f26741e926f46ae319ddc7c
















 上海工商
上海工商