锐角三角函数思维导图
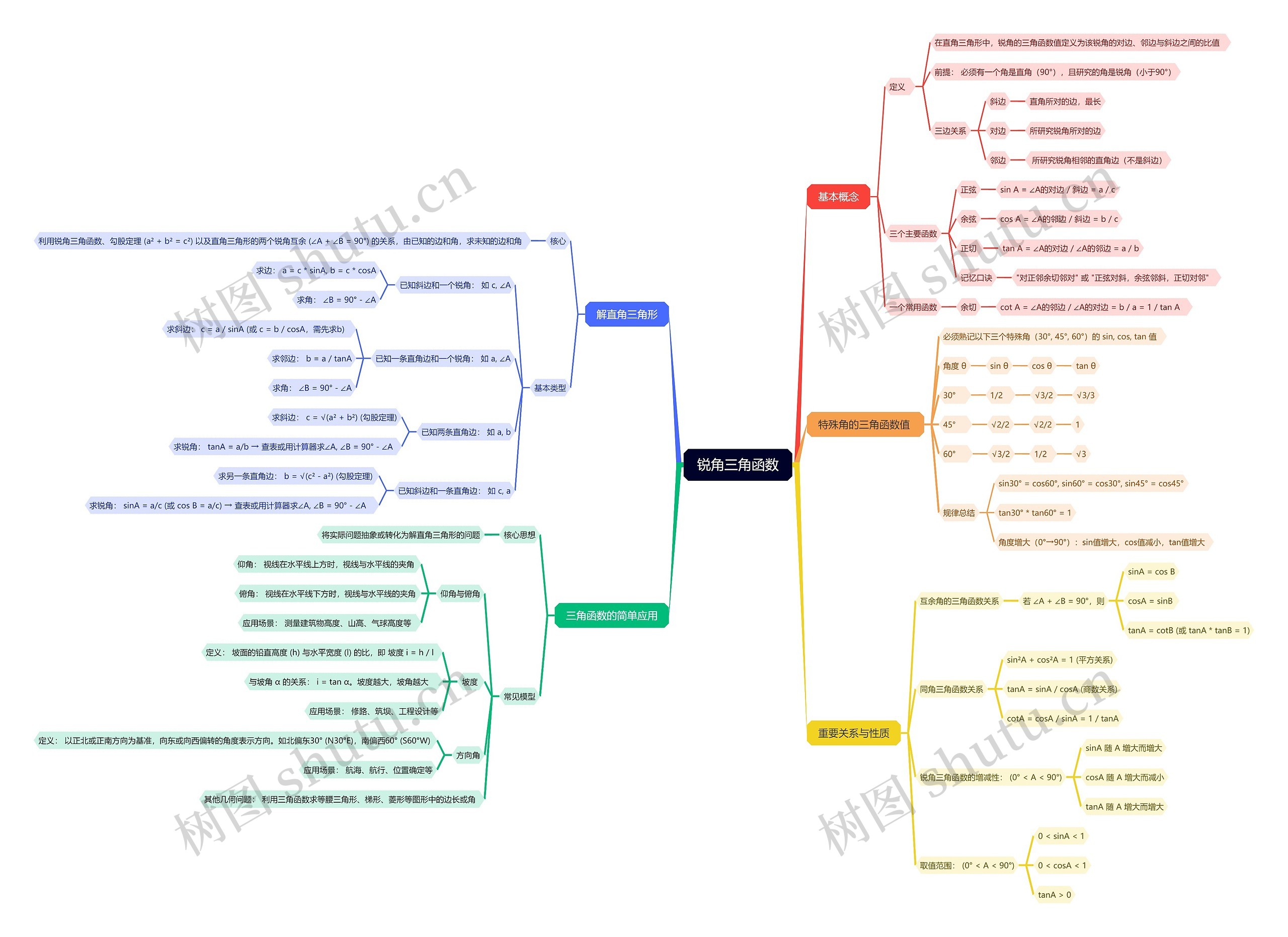
基本概念,三角函数值,函数应用相关内容讲解
树图思维导图提供 锐角三角函数 在线思维导图免费制作,点击“编辑”按钮,可对 锐角三角函数 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7438a7110fb919375bfe6b18a449389c
思维导图大纲
锐角三角函数思维导图模板大纲
基本概念
定义
在直角三角形中,锐角的三角函数值定义为该锐角的对边、邻边与斜边之间的比值
前提: 必须有一个角是直角(90°),且研究的角是锐角(小于90°)
三边关系
斜边
直角所对的边,最长
对边
所研究锐角所对的边
邻边
所研究锐角相邻的直角边(不是斜边)
三个主要函数
正弦
sin A = ∠A的对边 / 斜边 = a / c
余弦
cos A = ∠A的邻边 / 斜边 = b / c
正切
tan A = ∠A的对边 / ∠A的邻边 = a / b
记忆口诀
"对正邻余切邻对" 或 "正弦对斜,余弦邻斜,正切对邻"
一个常用函数
余切
cot A = ∠A的邻边 / ∠A的对边 = b / a = 1 / tan A
特殊角的三角函数值
必须熟记以下三个特殊角(30°, 45°, 60°)的 sin, cos, tan 值
角度 θ
sin θ
cos θ
tan θ
30°
1/2
√3/2
√3/3
45°
√2/2
√2/2
1
60°
√3/2
1/2
√3
规律总结
sin30° = cos60°, sin60° = cos30°, sin45° = cos45°
tan30° * tan60° = 1
角度增大(0°→90°):sin值增大,cos值减小,tan值增大
解直角三角形
核心
利用锐角三角函数、勾股定理 (a² + b² = c²) 以及直角三角形的两个锐角互余 (∠A + ∠B = 90°) 的关系,由已知的边和角,求未知的边和角
基本类型
已知斜边和一个锐角: 如 c, ∠A
求边: a = c * sinA, b = c * cosA
求角: ∠B = 90° - ∠A
已知一条直角边和一个锐角: 如 a, ∠A
求斜边: c = a / sinA (或 c = b / cosA,需先求b)
求邻边: b = a / tanA
求角: ∠B = 90° - ∠A
已知两条直角边: 如 a, b
求斜边: c = √(a² + b²) (勾股定理)
求锐角: tanA = a/b → 查表或用计算器求∠A, ∠B = 90° - ∠A
已知斜边和一条直角边: 如 c, a
求另一条直角边: b = √(c² - a²) (勾股定理)
求锐角: sinA = a/c (或 cos B = a/c) → 查表或用计算器求∠A, ∠B = 90° - ∠A
三角函数的简单应用
核心思想
将实际问题抽象或转化为解直角三角形的问题
常见模型
仰角与俯角
仰角: 视线在水平线上方时,视线与水平线的夹角
俯角: 视线在水平线下方时,视线与水平线的夹角
应用场景: 测量建筑物高度、山高、气球高度等
坡度
定义: 坡面的铅直高度 (h) 与水平宽度 (l) 的比,即 坡度 i = h / l
与坡角 α 的关系: i = tan α。坡度越大,坡角越大
应用场景: 修路、筑坝、工程设计等
方向角
定义: 以正北或正南方向为基准,向东或向西偏转的角度表示方向。如北偏东30° (N30°E),南偏西60° (S60°W)
应用场景: 航海、航行、位置确定等
其他几何问题: 利用三角函数求等腰三角形、梯形、菱形等图形中的边长或角
重要关系与性质
互余角的三角函数关系
若 ∠A + ∠B = 90°,则
sinA = cos B
cosA = sinB
tanA = cotB (或 tanA * tanB = 1)
同角三角函数关系
sin²A + cos²A = 1 (平方关系)
tanA = sinA / cosA (商数关系)
cotA = cosA / sinA = 1 / tanA
锐角三角函数的增减性: (0° < A < 90°)
sinA 随 A 增大而增大
cosA 随 A 增大而减小
tanA 随 A 增大而增大
取值范围: (0° < A < 90°)
0 < sinA < 1
0 < cosA < 1
tanA > 0
相关思维导图模板


树图思维导图提供 四年级下册数学第五单元思维导图 在线思维导图免费制作,点击“编辑”按钮,可对 四年级下册数学第五单元思维导图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c31814afc9b3c89d643cb5035c8bbfc4

树图思维导图提供 三角函数知识整理 在线思维导图免费制作,点击“编辑”按钮,可对 三角函数知识整理 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:827dc1792779a55f7d739b83c2f7cb63
















 上海工商
上海工商