七年级下册数学第九章知识点总结思维导图
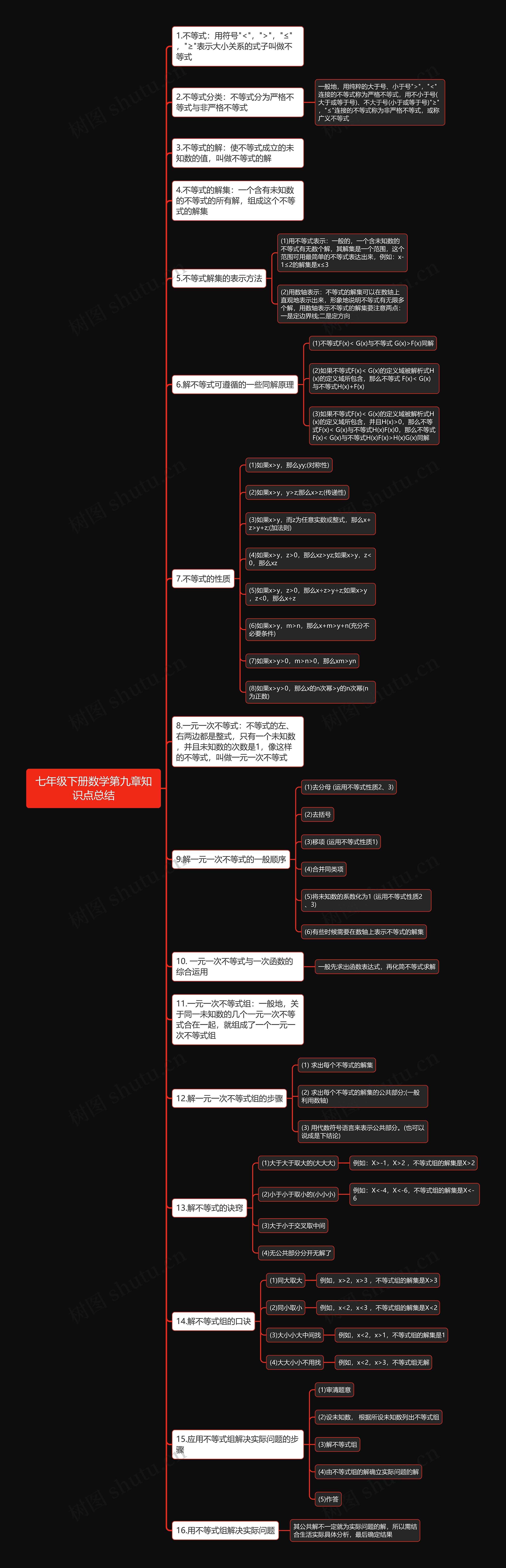
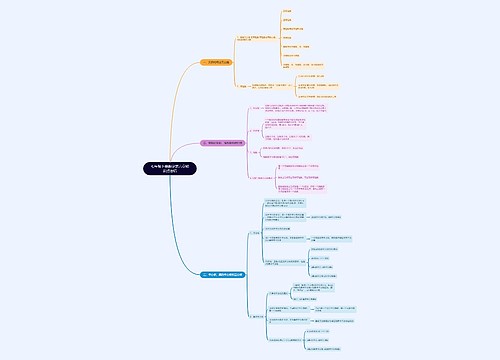
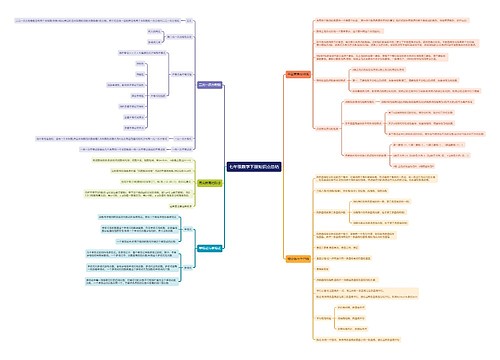
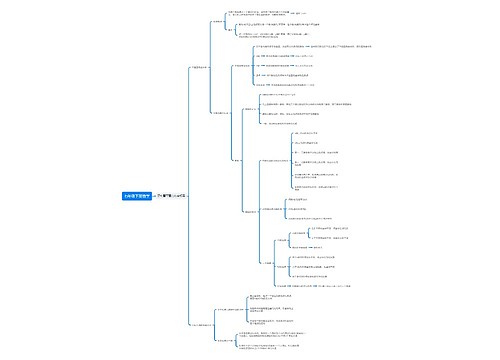
七年级下册数学第九章知识点总结思维导图包含以下知识点:不等式的表示方式、不等式的分类、不等式的解和解集、不等式解集的表示方式、解不等式可遵循的同解原理、不等式的性质、一元一次不等式和解法流程、一元一次不等式与一次函数的综合运用、一元一次不等式组和解法流程。需要注意数轴表示不等式解集的两点,即定边界线和定方向,解一元一次不等式时,一般需要进行去分母、去括号、移项、合并同类项、化系数,在解一元一次不等式组时,需要先求出每个不等式的解集,在求出他的公共部分,并用代数符号语言来表示公共部分。
思维导图大纲
七年级下册数学第九章知识点总结思维导图模板大纲
1.不等式:用符号"<",">","≤","≥"表示大小关系的式子叫做不等式
2.不等式分类:不等式分为严格不等式与非严格不等式
一般地,用纯粹的大于号、小于号">","<"连接的不等式称为严格不等式,用不小于号(大于或等于号)、不大于号(小于或等于号)"≥","≤"连接的不等式称为非严格不等式,或称广义不等式
3.不等式的解:使不等式成立的未知数的值,叫做不等式的解
4.不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集
5.不等式解集的表示方法
(1)用不等式表示:一般的,一个含未知数的不等式有无数个解,其解集是一个范围,这个范围可用最简单的不等式表达出来,例如:x-1≤2的解集是x≤3
(2)用数轴表示:不等式的解集可以在数轴上直观地表示出来,形象地说明不等式有无限多个解,用数轴表示不等式的解集要注意两点:一是定边界线;二是定方向
6.解不等式可遵循的一些同解原理
(1)不等式F(x)< G(x)与不等式 G(x)>F(x)同解
(2)如果不等式F(x)< G(x)的定义域被解析式H(x)的定义域所包含,那么不等式 F(x)< G(x)与不等式H(x)+F(x)
(3)如果不等式F(x)< G(x)的定义域被解析式H(x)的定义域所包含,并且H(x)>0,那么不等式F(x)< G(x)与不等式H(x)F(x)0,那么不等式F(x)< G(x)与不等式H(x)F(x)>H(x)G(x)同解
7.不等式的性质
(1)如果x>y,那么yy;(对称性)
(2)如果x>y,y>z;那么x>z;(传递性)
(3)如果x>y,而z为任意实数或整式,那么x+z>y+z;(加法则)
(4)如果x>y,z>0,那么xz>yz;如果x>y,z<0,那么xz
(5)如果x>y,z>0,那么x÷z>y÷z;如果x>y,z<0,那么x÷z
(6)如果x>y,m>n,那么x+m>y+n(充分不必要条件)
(7)如果x>y>0,m>n>0,那么xm>yn
(8)如果x>y>0,那么x的n次幂>y的n次幂(n为正数)
8.一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的次数是1,像这样的不等式,叫做一元一次不等式
9.解一元一次不等式的一般顺序
(1)去分母 (运用不等式性质2、3)
(2)去括号
(3)移项 (运用不等式性质1)
(4)合并同类项
(5)将未知数的系数化为1 (运用不等式性质2、3)
(6)有些时候需要在数轴上表示不等式的解集
10. 一元一次不等式与一次函数的综合运用
一般先求出函数表达式,再化简不等式求解
11.一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组
12.解一元一次不等式组的步骤
(1) 求出每个不等式的解集
(2) 求出每个不等式的解集的公共部分;(一般利用数轴)
(3) 用代数符号语言来表示公共部分。(也可以说成是下结论)
13.解不等式的诀窍
(1)大于大于取大的(大大大)
例如:X>-1,X>2 ,不等式组的解集是X>2
(2)小于小于取小的(小小小)
例如:X<-4,X<-6,不等式组的解集是X<-6
(3)大于小于交叉取中间
(4)无公共部分分开无解了
14.解不等式组的口诀
(1)同大取大
例如,x>2,x>3 ,不等式组的解集是X>3
(2)同小取小
例如,x<2,x<3 ,不等式组的解集是X<2
(3)大小小大中间找
例如,x<2,x>1,不等式组的解集是1
(4)大大小小不用找
例如,x<2,x>3,不等式组无解
15.应用不等式组解决实际问题的步骤
(1)审清题意
(2)设未知数,根据所设未知数列出不等式组
(3)解不等式组
(4)由不等式组的解确立实际问题的解
(5)作答
16.用不等式组解决实际问题
其公共解不一定就为实际问题的解,所以需结合生活实际具体分析,最后确定结果
相关思维导图模板

树图思维导图提供 初一数学教师下学期工作计划2020 在线思维导图免费制作,点击“编辑”按钮,可对 初一数学教师下学期工作计划2020 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:98bd9423e00ee537d40e3b9675b0b87f

树图思维导图提供 数学七年级下单元教学计划 在线思维导图免费制作,点击“编辑”按钮,可对 数学七年级下单元教学计划 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:18c5018b9a2ce52950f801586614a005
















 上海工商
上海工商