控制系统的数学模型脑图思维导图

控制系统的教学模型全内容详解
树图思维导图提供 控制系统的数学模型脑图 在线思维导图免费制作,点击“编辑”按钮,可对 控制系统的数学模型脑图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:bf52b6969a521729c4212966aa8f80da
思维导图大纲
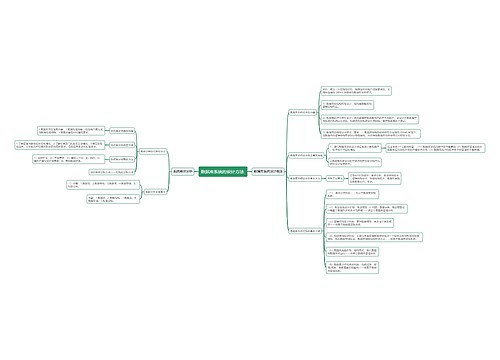
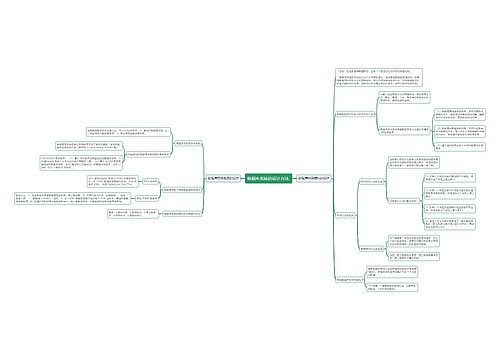
控制系统的数学模型思维导图模板大纲
微分方程
建立步骤
确定系统(或元件)的输入量,输出量
按照信号的传递顺序,根据各变量所遵循的运动规律列写各环节的动态方程,需考虑相邻元件间的负载效应,必要时考虑做线性化处理
消去中间变量,导出只含有输入量和输出量的系统微分方程
规范,整理微分方程,输出量放在方程的左侧,输入量放在方程的右侧,各阶导数项的阶次按降幂排列
非线性方程的线性化
传递函数
定义
在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比
术语
特征方程
阶数
极点
零点
形式
性质
传递函数与微分方程之间一一对应
G(s)取决于系统或原件的结构参数,与输入量形式无关
G(s)与输入信号的作用位置与输出信号的取出位有关
传递函数是复变量s的有理真分式函数m<=n,且具有复变量函数的所有性质。(物理可实现)
G(s)虽然描述了输出与输入之间的关系,但它不提供任何该系统的物理结构。因许多不同的物理系统具有完全相同的传递函数
令传递函数的分母多项式等于零所得到的方程称为系统的特征方程,即N(s)=0,特征方程的根就是传递函数的极点
传递函数G(s)的拉氏变换是脉冲响应g(t),脉冲响应g(t)是系统在单位脉冲输入的输出响应
典型环节
比例环节
积分环节
微分环节
惯性环节
一阶微分环节
二阶微分环节
二阶振荡环节
迟滞(时滞或延迟)环节
典型传递函数
系统对给定作用和扰动作用的传递函数
结构框图
绘制步骤
1,按照系统的结构和工作原理,分解出各环节并写出它的传递函数
2,绘制各环节的动态方框图,方框图中标明它的传递函数,并以箭头和字母符号表明其输入量和输出量,按照信号的传递方向把各方框图依次连接起来,就构成了系统结构图。
等效变换
串联,并联,反馈
分支点
前移
后移
相加点
前移
后移
变位
方框图四要素
方框(方块)
表示输入到输出单向传输间的函数关系
信号线
带有箭头的直线,箭头表示信号的流向,在直线旁边标记信号的时间函数或象函数
比较点(汇入点,综合点)
两个或两个以上的输入信号进行加减比较的元件。“+”表示相加,“-”表示相减,“+”可以省略不写
引出点(分支点,测量点)
表示信号测量或引出的位置
信号流图
术语
源点,汇点,混合节点
通路,开通路,闭通路,前向通路
不接触回环
绘制
简化
梅森公式
形式
n:前向通路数
Pk:第k条前向通路增益
▲:信号流图特征式
求传递函数的步骤
确定框图的回路及其增益
确定互不接触回路及其增益
求取特征式A(s)
确定前向通道增益及其余子式
代入梅森公式并整理
性质
信号流图适用于线性系统(传递函数一样)
支路表示一个信号对另一个信号的函数关系,信号只能沿支路上的箭头指向传递
在节点上可以把所有输入支路的信号叠加,并把相加后的信号送到所有的输入支路
具有输入和输出节点,通过增加一个具有单位增益的支路把它作为输入节点来处理
对于一个给定的系统,信号流图不是唯一的,由于描述同一个系统的方程可以表示为不同的形式










 上海工商
上海工商