高考数学圆锥曲线解题技巧思维导图
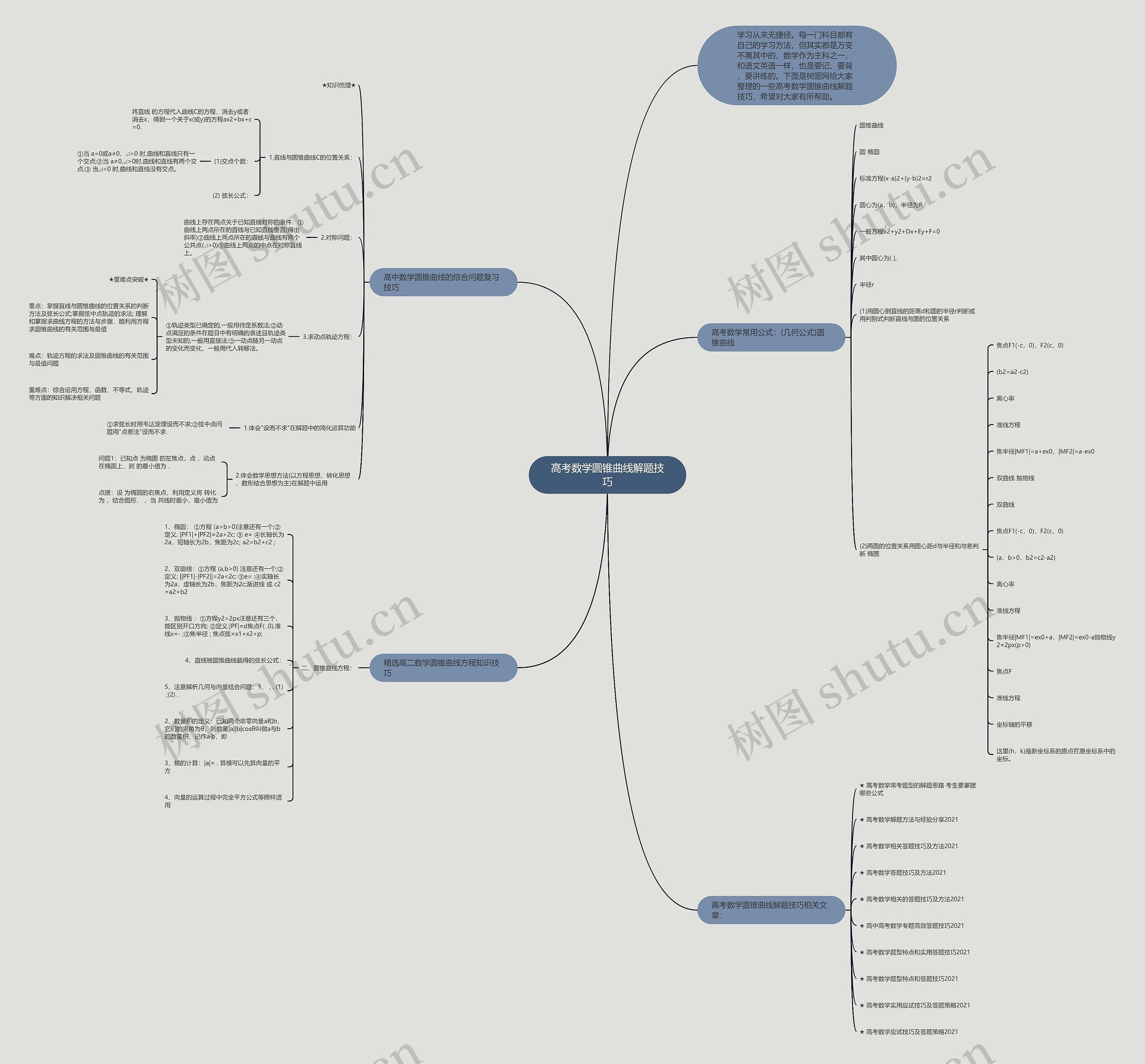
高考数学圆锥曲线解题技巧思维导图模板展示了高中数学圆锥曲线的解题技巧,首先要掌握直线与圆锥曲线的位置关系的判断方法及弦长公式,掌握弦中点轨迹的求法和理解和掌握求曲线方程的方法与步骤,轨迹方程的求法及圆锥曲线的有关范围与最值问题也是难点,综合运用方程、函数、不等式、轨迹的知识来解决相关问题的重要性,和具体的数学思想方法和常用公式。
思维导图大纲
高考数学圆锥曲线解题技巧思维导图模板大纲
学习从来无捷径。每一门科目都有自己的学习方法,但其实都是万变不离其中的,数学作为主科之一,和语文英语一样,也是要记、要背、要讲练的。下面是树图网给大家整理的一些高考数学圆锥曲线解题技巧,希望对大家有所帮助。
高中数学圆锥曲线的综合问题复习技巧
★知识梳理★
1.直线与圆锥曲线C的位置关系:
将直线 的方程代入曲线C的方程,消去y或者消去x,得到一个关于x(或y)的方程ax2+bx+c=0.
(1)交点个数:
①当 a=0或a≠0,⊿=0 时,曲线和直线只有一个交点;②当 a≠0,⊿>0时,曲线和直线有两个交点;③ 当⊿<0 时,曲线和直线没有交点。
(2) 弦长公式:
2.对称问题:
曲线上存在两点关于已知直线对称的条件:①曲线上两点所在的直线与已知直线垂直(得出斜率)②曲线上两点所在的直线与曲线有两个公共点(⊿>0)③曲线上两点的中点在对称直线上。
3.求动点轨迹方程:
①轨迹类型已确定的,一般用待定系数法;②动点满足的条件在题目中有明确的表述且轨迹类型未知的,一般用直接法;③一动点随另一动点的变化而变化,一般用代入转移法。
★重难点突破★
重点:掌握直线与圆锥曲线的位置关系的判断方法及弦长公式;掌握弦中点轨迹的求法; 理解和掌握求曲线方程的方法与步骤,能利用方程求圆锥曲线的有关范围与最值
难点:轨迹方程的求法及圆锥曲线的有关范围与最值问题
重难点:综合运用方程、函数、不等式、轨迹等方面的知识解决相关问题
1.体会"设而不求"在解题中的简化运算功能
①求弦长时用韦达定理设而不求;②弦中点问题用"点差法"设而不求.
2.体会数学思想方法(以方程思想、转化思想、数形结合思想为主)在解题中运用
问题1:已知点 为椭圆 的左焦点,点 ,动点 在椭圆上,则 的最小值为 .
点拨:设 为椭圆的右焦点,利用定义将 转化为 ,结合图形, ,当 共线时最小,最小值为
高考数学常用公式:(几何公式)圆锥曲线
圆锥曲线
圆 椭圆
标准方程(x-a)2+(y-b)2=r2
圆心为(a,b),半径为R
一般方程x2+y2+Dx+Ey+F=0
其中圆心为( ),
半径r
(1)用圆心到直线的距离d和圆的半径r判断或用判别式判断直线与圆的位置关系
(2)两圆的位置关系用圆心距d与半径和与差判断 椭圆
焦点F1(-c,0),F2(c,0)
(b2=a2-c2)
离心率
准线方程
焦半径|MF1|=a+ex0,|MF2|=a-ex0
双曲线 抛物线
双曲线
焦点F1(-c,0),F2(c,0)
(a,b>0,b2=c2-a2)
离心率
准线方程
焦半径|MF1|=ex0+a,|MF2|=ex0-a抛物线y2=2px(p>0)
焦点F
准线方程
坐标轴的平移
这里(h,k)是新坐标系的原点在原坐标系中的坐标。
精选高二数学圆锥曲线方程知识技巧
二、圆锥曲线方程:
1、椭圆: ①方程 (a>b>0)注意还有一个;②定义: |PF1|+|PF2|=2a>2c; ③ e= ④长轴长为2a,短轴长为2b,焦距为2c; a2=b2+c2 ;
2、双曲线:①方程 (a,b>0) 注意还有一个;②定义: ||PF1|-|PF2||=2a<2c; ③e= ;④实轴长为2a,虚轴长为2b,焦距为2c;渐进线 或 c2=a2+b2
3、抛物线 :①方程y2=2px注意还有三个,能区别开口方向; ②定义:|PF|=d焦点F( ,0),准线x=- ;③焦半径 ; 焦点弦=x1+x2+p;
4、直线被圆锥曲线截得的弦长公式:
5、注意解析几何与向量结合问题:1、 , . (1) ;(2) .
2、数量积的定义:已知两个非零向量a和b,它们的夹角为θ,则数量|a||b|cosθ叫做a与b的数量积,记作a·b,即
3、模的计算:|a|= . 算模可以先算向量的平方
4、向量的运算过程中完全平方公式等照样适用
高考数学圆锥曲线解题技巧相关文章:
★ 高考数学常考题型的解题思路 考生要掌握哪些公式
★ 高考数学解题方法与经验分享2021
★ 高考数学相关答题技巧及方法2021
★ 高考数学答题技巧及方法2021
★ 高考数学相关的答题技巧及方法2021
★ 高中高考数学专题高效答题技巧2021
★ 高考数学题型特点和实用答题技巧2021
★ 高考数学题型特点和答题技巧2021
★ 高考数学实用应试技巧及答题策略2021
★ 高考数学应试技巧及答题策略2021
相关思维导图模板

树图思维导图提供 数学圆锥曲线题解题技巧方法 在线思维导图免费制作,点击“编辑”按钮,可对 数学圆锥曲线题解题技巧方法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6237e79838d2b13b1c8479e316428669

树图思维导图提供 高考数学考场答题技巧:解析几何解题方法 在线思维导图免费制作,点击“编辑”按钮,可对 高考数学考场答题技巧:解析几何解题方法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1ab01875539f49e56c26a7002078bc7b




















 上海工商
上海工商