机械振动和机械波思维导图
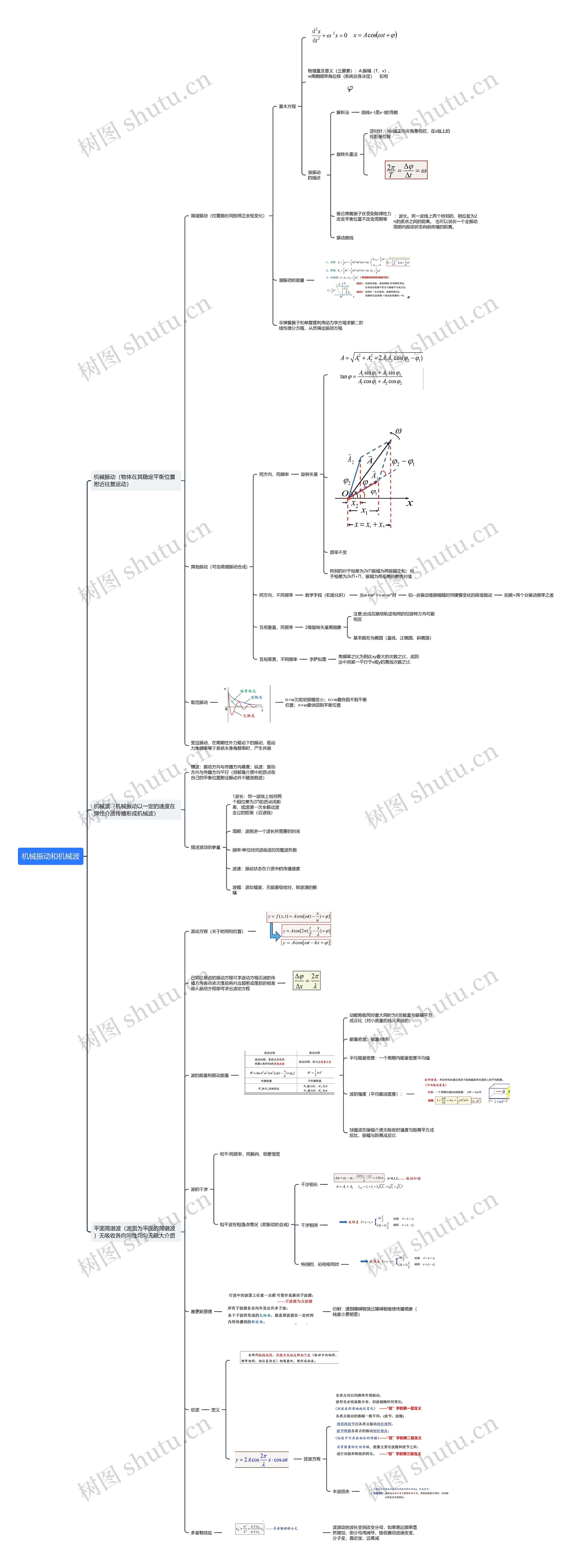
机械振动和机械波
树图思维导图提供 机械振动和机械波 在线思维导图免费制作,点击“编辑”按钮,可对 机械振动和机械波 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a3d3c0874dc172fdbc8478c70d2ae318
思维导图大纲
机械振动和机械波思维导图模板大纲
机械振动(物体在其稳定平衡位置附近往复运动)
简谐振动(位置随时间按照正余弦变化)
基本方程
物理量及意义(三要素):A:振幅(T,v),w周期频率角位移 (系统自身决定) 初相
谐振动的描述
解析法
曲线v-t是x-t的导数
旋转矢量法
逆时针,与x轴正向夹角是相位,在x轴上的投影是位移
推论弹簧振子在受到除弹性力以外的恒力时只改变平衡位置不改变周期等
振动曲线
谐振动的能量
非弹簧振子和单复摆利用动力学方程求解二阶线性微分方程,从而得出振动方程
其他振动(可由简谐振动合成)
同方向,同频率
旋转矢量
频率不变
特别的对于相差为2kΠ振幅为两振幅之和;对于相差为2kΠ+Π,振幅为两相差的差绝对值
同方向,不同频率
数学手段(和差化积)
当w+w*>>w-w*时
拍--合振动是振幅随时间缓慢变化的简谐振动
拍频=两个分振动频率之差
互相垂直,同频率
2维旋转矢量画图象
注意;合成后振动轨迹相同的但旋转方向可能相反
基本图形为椭圆(直线,正椭圆,斜椭圆)
互相垂直,不同频率
李萨如图
角频率之比为到达xy最大的次数之比,或到达中间某一平行于x或y的直线次数之比
阻尼振动
n<w欠阻尼振幅变小;n>w最终回不到平衡位置;n=w最快回到平衡位置
受迫振动,在周期性外力驱动下的振动,驱动力角频率等于系统本身角频率时,产生共振
机械波(机械振动以一定的速度在弹性介质传播形成机械波)
横波:振动方向与传播方向垂直;纵波:振动方向与传播方向平行(但都是介质中的质点在自己的平衡位置附近振动并不随波前进)
描述波动的参量
1波长:同一波线上相邻两个相位差为2Π的质点间距离,或波源一次全振动波走过的距离(沿波线)
周期:波前进一个波长所需要的时间
频率:单位时间波前进的完整波形数
波速:振动状态在介质中的传播速度
波幅:波动幅度,无能量吸收时,即波源的振幅
平面简谐波(波面为平面的简谐波)无吸收各向同性均匀无限大介质
波动方程(关于时间和位置)
已知任意点的振动方程可求波动方程沿波的传播方向各点依次落后将对应超前或落后的相差带入振动方程即可求出波动方程
波的能量和振动能量
动能势能同时最大同时为0总能量与振幅平方成正比(对小质量的线元来说的)
能量密度:能量/体积
平均能量密度:一个周期内能量密度平均值
波的强度(平均能流密度):
球面波在振幅介质无吸收时强度与距离平方成反比,振幅与距离成反比
波的干涉
相干:同频率,同振向,相差恒定
相干波在相遇点情况(即振动的合成)
干涉相长
干涉相消
特别的,初相相同时
惠更斯原理
衍射:遇到障碍物饶过障碍物继续传播现象(线度小更明显)
驻波
定义
驻波方程
半波损失
多普勒效应
波源动则波长变则改变分母,如果靠近频率显然增加,则分母用减号,接收器动波速改变,分子变,靠近加,远离减
:波长。同一波线上两个相邻的、相位差为2π的质点之间的距离。 也可以说在一个全振动周期内振动状态向前传播的距离。 思维导图模板大纲
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 光和影 在线思维导图免费制作,点击“编辑”按钮,可对 光和影 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:2f4c9606f70a3f8d98ec4d65695dc3d1









 上海工商
上海工商