初一数学和圆有关的知识点思维导图
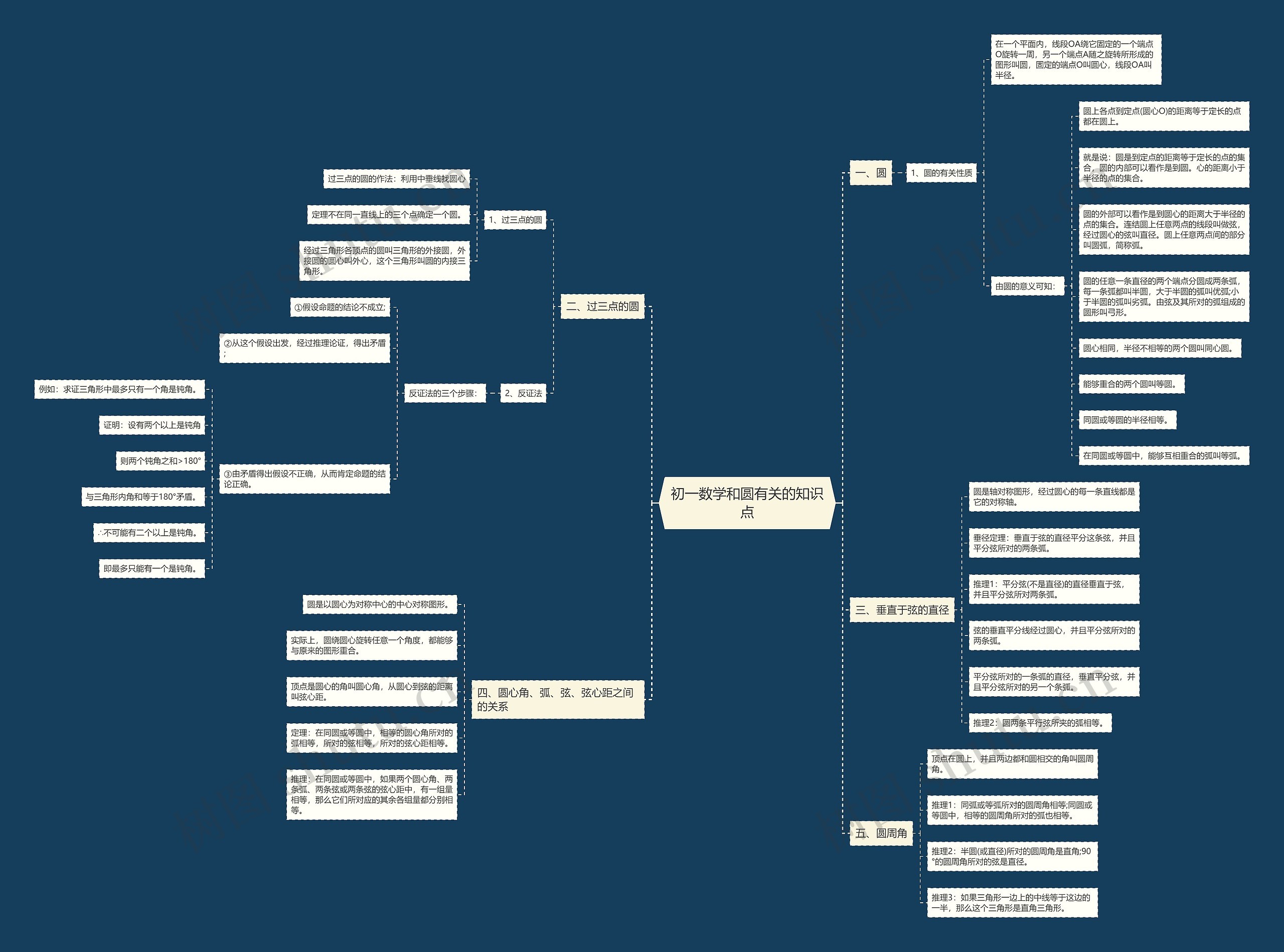
初一数学和圆有关的知识点思维导图包含圆的有关性质、圆心角、弧、弦、弦心距之间的关系、过三点的圆及反证法、垂直于弦的直径。圆可以由固定的一个端点O和绕O旋转一周的另一点A形成,而线段OA则是圆的半径,连结圆上任意两点的线段是弦,经过圆心的弦是直径,圆内是到圆心距离小于半径的点集合,圆外是到圆心距离大于半径的点集合。同心圆是圆心相同但半径不同的两个圆,等圆是能够重合的两个圆。通过中垂线可以找到过三个不在同一直线上的点的圆心,反证法的三个步骤,假设命题的结论不成立,从此推理得出矛盾,由矛盾得出假设不正确,因此命题的结论就成立了。垂直于弦的直径平分弦,平分弦所对的两条弧,在同圆或等圆中,相等的圆心角所对的弧、弦和弦心距也相等。
思维导图大纲
初一数学和圆有关的知识点思维导图模板大纲
一、圆
1、圆的有关性质
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆,固定的端点O叫圆心,线段OA叫半径。
由圆的意义可知:
圆上各点到定点(圆心O)的距离等于定长的点都在圆上。
就是说:圆是到定点的距离等于定长的点的集合,圆的内部可以看作是到圆。心的距离小于半径的点的集合。
圆的外部可以看作是到圆心的距离大于半径的点的集合。连结圆上任意两点的线段叫做弦,经过圆心的弦叫直径。圆上任意两点间的部分叫圆弧,简称弧。
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫半圆,大于半圆的弧叫优弧;小于半圆的弧叫劣弧。由弦及其所对的弧组成的圆形叫弓形。
圆心相同,半径不相等的两个圆叫同心圆。
能够重合的两个圆叫等圆。
同圆或等圆的半径相等。
在同圆或等圆中,能够互相重合的弧叫等弧。
二、过三点的圆
1、过三点的圆
过三点的圆的作法:利用中垂线找圆心
定理不在同一直线上的三个点确定一个圆。
经过三角形各顶点的圆叫三角形的外接圆,外接圆的圆心叫外心,这个三角形叫圆的内接三角形。
2、反证法
反证法的三个步骤:
①假设命题的结论不成立;
②从这个假设出发,经过推理论证,得出矛盾;
③由矛盾得出假设不正确,从而肯定命题的结论正确。
例如:求证三角形中最多只有一个角是钝角。
证明:设有两个以上是钝角
则两个钝角之和>180°
与三角形内角和等于180°矛盾。
∴不可能有二个以上是钝角。
即最多只能有一个是钝角。
三、垂直于弦的直径
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
推理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对两条弧。
弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一个条弧。
推理2:圆两条平行弦所夹的弧相等。
四、圆心角、弧、弦、弦心距之间的关系
圆是以圆心为对称中心的中心对称图形。
实际上,圆绕圆心旋转任意一个角度,都能够与原来的图形重合。
顶点是圆心的角叫圆心角,从圆心到弦的距离叫弦心距。
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
推理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等。
五、圆周角
顶点在圆上,并且两边都和圆相交的角叫圆周角。
推理1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
推理2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
推理3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
相关思维导图模板

树图思维导图提供 数学九年级上册知识点 在线思维导图免费制作,点击“编辑”按钮,可对 数学九年级上册知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:28baa381efe3d143749b39bba985cd3c


树图思维导图提供 2023初一数学几何的初步知识知识点整理 在线思维导图免费制作,点击“编辑”按钮,可对 2023初一数学几何的初步知识知识点整理 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7c866a0b09c5abb819866c7f8527f413



















 上海工商
上海工商