高一数学解题点拨 高一数学解题方法思维导图
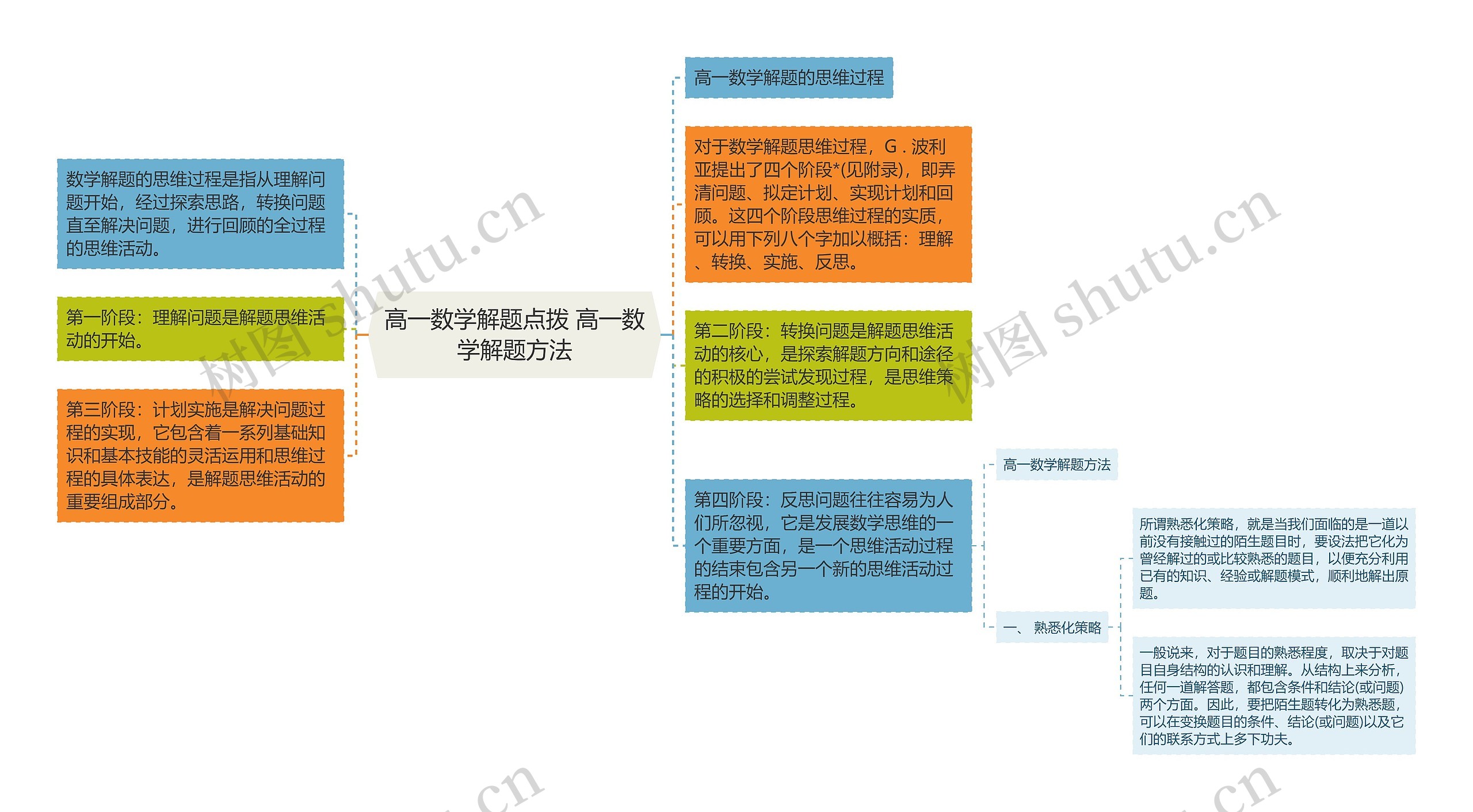
高一数学解题的思维过程包含理解问题、转换问题、实施计划和反思问题四个阶段,分别对应着解题的开始、核心、实现和结束。理解问题是解题的起点,在转换问题阶段需要积极探索解题的方向和途径,选择和调整思维策略,实施计划是解决问题的具体实现,需要灵活运用基础知识和基本技能。而反思问题则忽视,但他是发展数学思维的重要方面,是一个思维活动的结束和新的思维活动的开始。
高一数学解题方法中,熟悉化策略是指当遇到陌生题目时,要设法将其转化为已知的或熟悉的题目,以便利用已有的知识、经验或解题模式来解决原题。理解题目的结构对于熟悉化策略的重要性不可忽视,每道解答题都包含条件和结论(或问题)两个方面,可以通过变换题目的条件、结论(或问题)和他们的联系方式来将陌生题目转化为熟悉的题目,这样就可以更顺利地解决原题。
思维导图大纲
高一数学解题点拨 高一数学解题方法思维导图模板大纲
高一数学解题的思维过程
数学解题的思维过程是指从理解问题开始,经过探索思路,转换问题直至解决问题,进行回顾的全过程的思维活动。
对于数学解题思维过程,G . 波利亚提出了四个阶段*(见附录),即弄清问题、拟定计划、实现计划和回顾。这四个阶段思维过程的实质,可以用下列八个字加以概括:理解、转换、实施、反思。
第一阶段:理解问题是解题思维活动的开始。
第二阶段:转换问题是解题思维活动的核心,是探索解题方向和途径的积极的尝试发现过程,是思维策略的选择和调整过程。
第三阶段:计划实施是解决问题过程的实现,它包含着一系列基础知识和基本技能的灵活运用和思维过程的具体表达,是解题思维活动的重要组成部分。
第四阶段:反思问题往往容易为人们所忽视,它是发展数学思维的一个重要方面,是一个思维活动过程的结束包含另一个新的思维活动过程的开始。
高一数学解题方法
一、 熟悉化策略
所谓熟悉化策略,就是当我们面临的是一道以前没有接触过的陌生题目时,要设法把它化为曾经解过的或比较熟悉的题目,以便充分利用已有的知识、经验或解题模式,顺利地解出原题。
一般说来,对于题目的熟悉程度,取决于对题目自身结构的认识和理解。从结构上来分析,任何一道解答题,都包含条件和结论(或问题)两个方面。因此,要把陌生题转化为熟悉题,可以在变换题目的条件、结论(或问题)以及它们的联系方式上多下功夫。
相关思维导图模板

树图思维导图提供 高一二学生谈谈数学的学习方法 在线思维导图免费制作,点击“编辑”按钮,可对 高一二学生谈谈数学的学习方法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:37cb3118dbe1d156b584a20563577324

树图思维导图提供 优秀高一数学等差数列教案 在线思维导图免费制作,点击“编辑”按钮,可对 优秀高一数学等差数列教案 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c2e05029afc4f4c5193914cd21fdfc27


















 上海工商
上海工商