高一数学:第三章函数的应用思维导图
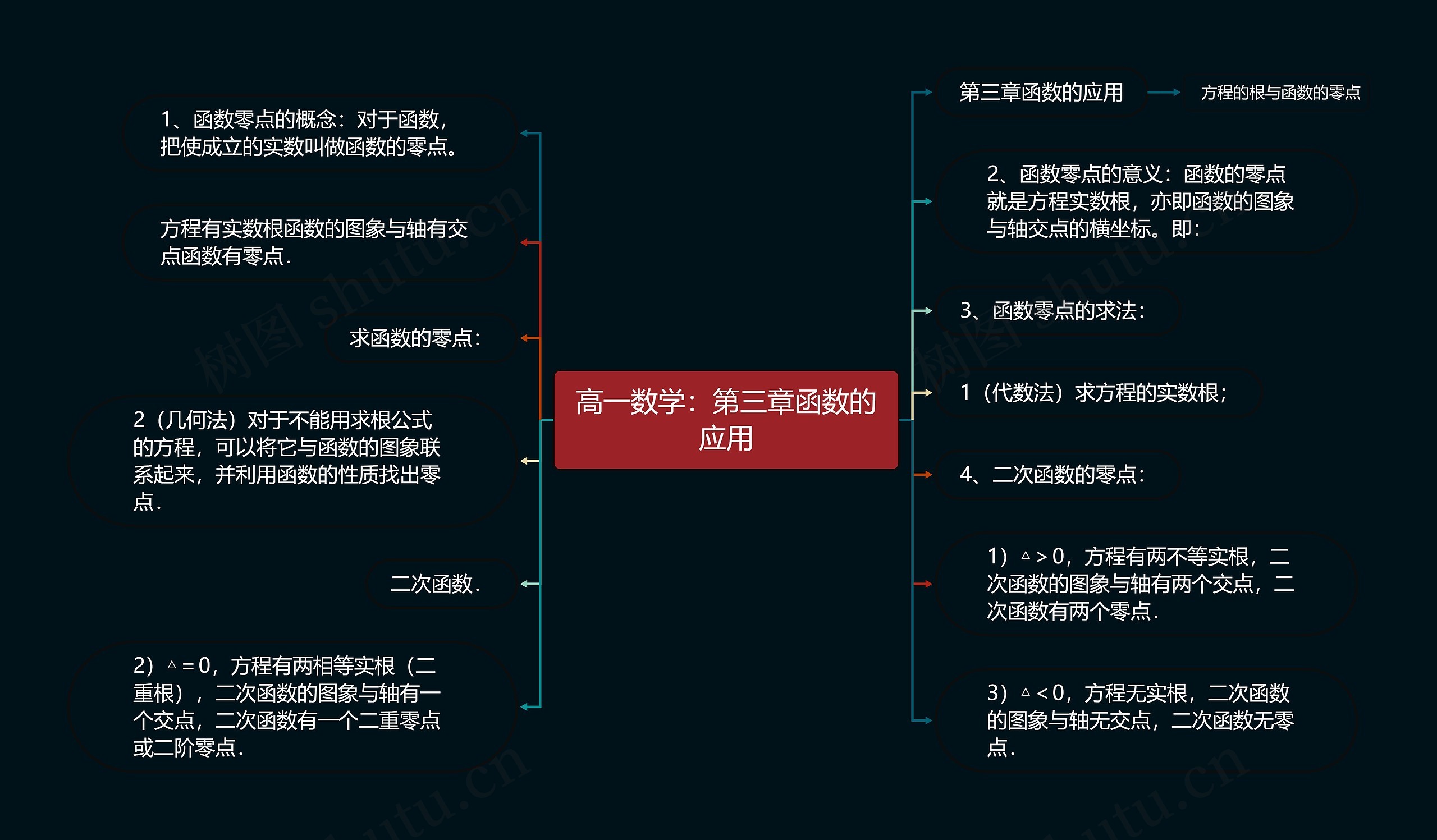
高一数学:第三章函数的应用思维导图是一篇介绍函数零点概念和求法的模板大纲,我们学习到了以下知识点:
1.函数零点/的概念:对于函数,使得函数成立的实数称为函数的零点。
2.函数零点/的意义:函数的零点即为方程的实数根,也就是函数图象与坐标轴交点的横坐标。
3.函数零点/的求法:
a)代数法:通过求解方程的实数根来寻找函数的零点。
b)几何法:对于无法使用求根公式的方程,可以将其与函数的图象联系起来,并利用函数的性质来找到零点。
4.二次函数的零点:
a)当判别式△大于0时,方程有两个不相等的实根,二次函数的图象与坐标轴有两个交点,即二次函数有两个零点。
b)当判别式△等于0时,方程有两个相等的实根(即二重根),二次函数的图象与坐标轴有一个交点,即二次函数有一个二重零点或二阶零点。
c)/当判别式△小于0时,方程没有实根,二次函数的图象与坐标轴没有交点,即二次函数没有零点。
通过掌握这些知识点,可以更好的理解和应用函数的零点概念,解决与函数相关的问题。
思维导图大纲
高一数学:第三章函数的应用思维导图模板大纲
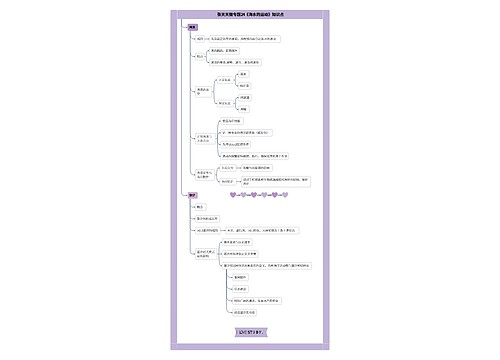
第三章函数的应用
方程的根与函数的零点
1、函数零点的概念:对于函数,把使成立的实数叫做函数的零点。
2、函数零点的意义:函数的零点就是方程实数根,亦即函数的图象与轴交点的横坐标。即:
方程有实数根函数的图象与轴有交点函数有零点.
3、函数零点的求法:
求函数的零点:
1(代数法)求方程的实数根;
2(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点.
4、二次函数的零点:
二次函数.
1)△>0,方程有两不等实根,二次函数的图象与轴有两个交点,二次函数有两个零点.
2)△=0,方程有两相等实根(二重根),二次函数的图象与轴有一个交点,二次函数有一个二重零点或二阶零点.
3)△<0,方程无实根,二次函数的图象与轴无交点,二次函数无零点.
相关思维导图模板

树图思维导图提供 高一数学第三章知识点总结:函数的应用 在线思维导图免费制作,点击“编辑”按钮,可对 高一数学第三章知识点总结:函数的应用 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:5ac6e37b15343a3f6d805c335dcf8ea1

树图思维导图提供 高一数学教学计划 在线思维导图免费制作,点击“编辑”按钮,可对 高一数学教学计划 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:65fb264ae8fb34544b3f231e8decb7a7








 上海工商
上海工商