高二数学复习方法:"充要条件"具体概念思维导图
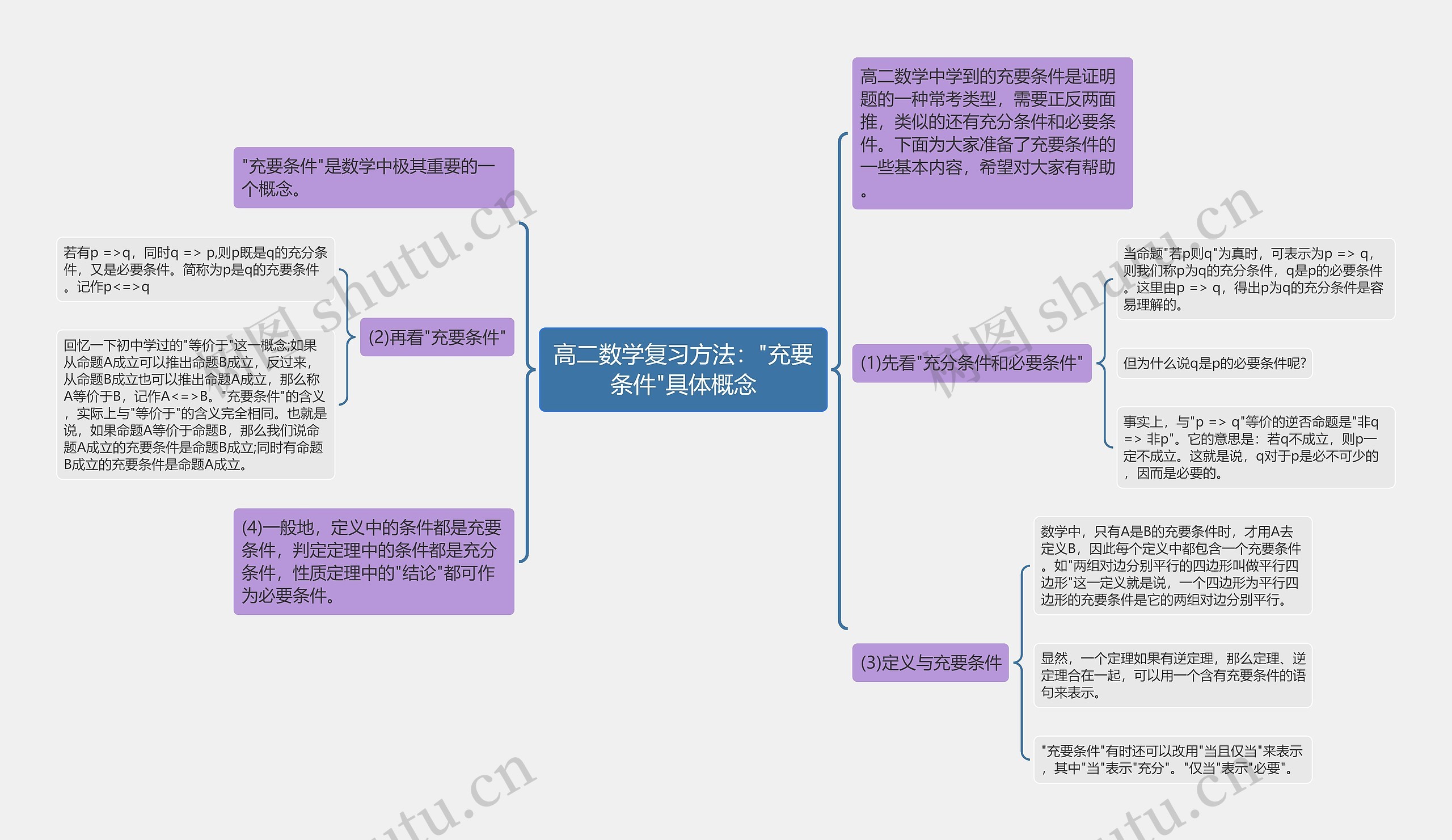
模板展示了高二数学复习方法中的“充要条件”具体概念思维导图,在高二数学中,充要条件是一种常考类型的证明题,需要进行正反两方面的推导,类似的还有充分条件和必要条件,充分条件和必要条件的概念,并说明了他之间的关系。充分条件是指若p成立,则q成立,而必要条件则是指若q不成立,则p一定不成立,充要条件的概念,即若p成立当且仅当q成立,思维导图模板还提到在数学中,只有A是B的充要条件时,才可以用A来定义B,因此每个定义中都包含一个充要条件。一般情况下,定义中的条件是充要条件,判定定理中的条件是充分条件,而性质定理中的结论可作为必要条件,这些知识点对于高二数学的复习非常有帮助。
思维导图大纲
高二数学复习方法:"充要条件"具体概念思维导图模板大纲
高二数学中学到的充要条件是证明题的一种常考类型,需要正反两面推,类似的还有充分条件和必要条件。下面为大家准备了充要条件的一些基本内容,希望对大家有帮助。
"充要条件"是数学中极其重要的一个概念。
(1)先看"充分条件和必要条件"
当命题"若p则q"为真时,可表示为p => q,则我们称p为q的充分条件,q是p的必要条件。这里由p => q,得出p为q的充分条件是容易理解的。
但为什么说q是p的必要条件呢?
事实上,与"p => q"等价的逆否命题是"非q => 非p"。它的意思是:若q不成立,则p一定不成立。这就是说,q对于p是必不可少的,因而是必要的。
(2)再看"充要条件"
若有p =>q,同时q => p,则p既是q的充分条件,又是必要条件。简称为p是q的充要条件。记作p<=>q
回忆一下初中学过的"等价于"这一概念;如果从命题A成立可以推出命题B成立,反过来,从命题B成立也可以推出命题A成立,那么称A等价于B,记作A<=>B。"充要条件"的含义,实际上与"等价于"的含义完全相同。也就是说,如果命题A等价于命题B,那么我们说命题A成立的充要条件是命题B成立;同时有命题B成立的充要条件是命题A成立。
(3)定义与充要条件
数学中,只有A是B的充要条件时,才用A去定义B,因此每个定义中都包含一个充要条件。如"两组对边分别平行的四边形叫做平行四边形"这一定义就是说,一个四边形为平行四边形的充要条件是它的两组对边分别平行。
显然,一个定理如果有逆定理,那么定理、逆定理合在一起,可以用一个含有充要条件的语句来表示。
"充要条件"有时还可以改用"当且仅当"来表示,其中"当"表示"充分"。"仅当"表示"必要"。
(4)一般地,定义中的条件都是充要条件,判定定理中的条件都是充分条件,性质定理中的"结论"都可作为必要条件。
相关思维导图模板

树图思维导图提供 高二数学复习方法:数学最容易丢分的33个知识点 在线思维导图免费制作,点击“编辑”按钮,可对 高二数学复习方法:数学最容易丢分的33个知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:3af053975ef9ba450d1af034cfb1cdfe

树图思维导图提供 人教版高中数学优秀教学设计 在线思维导图免费制作,点击“编辑”按钮,可对 人教版高中数学优秀教学设计 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:96a1c91dec73c2f244f0fff748eaa566



















 上海工商
上海工商