高考数学考场答题技巧:立体几何解题方法思维导图
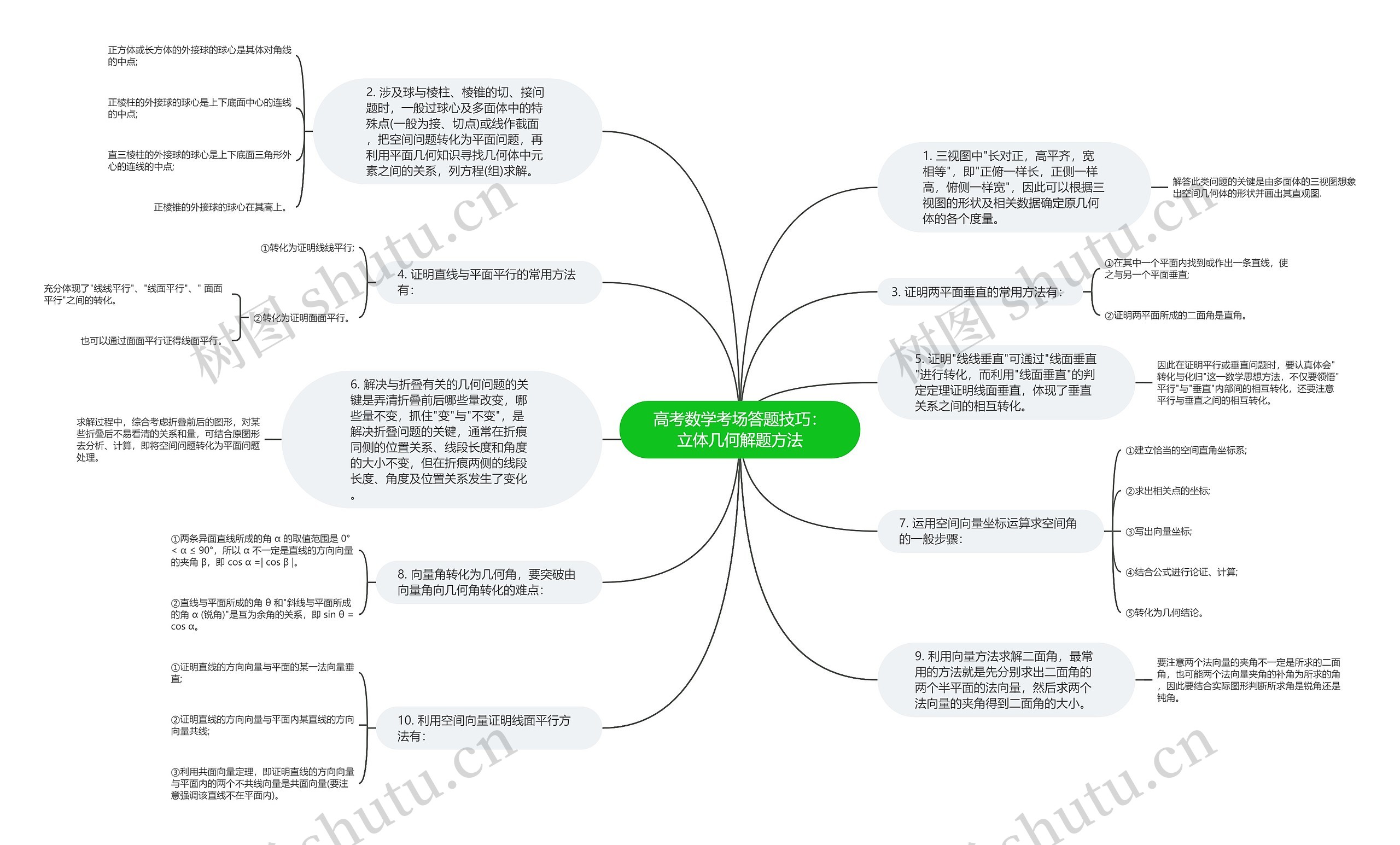
高考数学考场答题技巧:立体几何解题方法思维导图包含以下知识点:1.三视图的形状和数据可以确定原几何体的度量。
2.利用球与棱柱、棱锥的切、接问题,可以将空间问题转化为平面问题,通过平面几何知识求解。
3.证明两平面垂直的方法包含在其中一个平面内找到或作出一条直线与另一个平面垂直,和证明两平面所成二面角为直角。
4.证明直线与平面平行的方法包含转化为证明线线平行,转化为证明面面平行,和通过面面平行证得线面平行。
5.证明线线垂直可以通过线面垂直进行转化,利用线面垂直的判定定理证明线面垂直,体现了垂直关系之间的相互转化。
6.解决与折叠有关的几何问题的关键是弄清折叠前后哪些量改变,哪些量不变,抓住变与不变。折叠前后在折痕同侧的位置关系、线段长度和角度的大小不变,但在折痕两侧的线段长度、角度及位置关系发生了变化。
7.运用空间向量坐标运算求解空间角的一般步骤包含建立适当的空间直角坐标系、求出相关点的坐标、写出向量坐标、结合公式进行论证和计算,并转化为几何结论。
思维导图大纲
高考数学考场答题技巧:立体几何解题方法思维导图模板大纲
1. 三视图中"长对正,高平齐,宽相等",即"正俯一样长,正侧一样高,俯侧一样宽",因此可以根据三视图的形状及相关数据确定原几何体的各个度量。
解答此类问题的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.
2. 涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素之间的关系,列方程(组)求解。
正方体或长方体的外接球的球心是其体对角线的中点;
正棱柱的外接球的球心是上下底面中心的连线的中点;
直三棱柱的外接球的球心是上下底面三角形外心的连线的中点;
正棱锥的外接球的球心在其高上。
3. 证明两平面垂直的常用方法有:
①在其中一个平面内找到或作出一条直线,使之与另一个平面垂直;
②证明两平面所成的二面角是直角。
4. 证明直线与平面平行的常用方法有:
①转化为证明线线平行;
②转化为证明面面平行。
充分体现了"线线平行"、"线面平行"、" 面面平行"之间的转化。
也可以通过面面平行证得线面平行。
5. 证明"线线垂直"可通过"线面垂直"进行转化,而利用"线面垂直"的判定定理证明线面垂直,体现了垂直关系之间的相互转化。
因此在证明平行或垂直问题时,要认真体会"转化与化归"这一数学思想方法,不仅要领悟"平行"与"垂直"内部间的相互转化,还要注意平行与垂直之间的相互转化。
6. 解决与折叠有关的几何问题的关键是弄清折叠前后哪些量改变,哪些量不变,抓住"变"与"不变",是解决折叠问题的关键,通常在折痕同侧的位置关系、线段长度和角度的大小不变,但在折痕两侧的线段长度、角度及位置关系发生了变化。
求解过程中,综合考虑折叠前后的图形,对某些折叠后不易看清的关系和量,可结合原图形去分析、计算,即将空间问题转化为平面问题处理。
7. 运用空间向量坐标运算求空间角的一般步骤:
①建立恰当的空间直角坐标系;
②求出相关点的坐标;
③写出向量坐标;
④结合公式进行论证、计算;
⑤转化为几何结论。
8. 向量角转化为几何角,要突破由向量角向几何角转化的难点:
①两条异面直线所成的角 α 的取值范围是 0°< α ≤ 90°,所以 α 不一定是直线的方向向量的夹角 β,即 cos α =| cos β |。
②直线与平面所成的角 θ 和"斜线与平面所成的角 α (锐角)"是互为余角的关系,即 sin θ =cos α。
9. 利用向量方法求解二面角,最常用的方法就是先分别求出二面角的两个半平面的法向量,然后求两个法向量的夹角得到二面角的大小。
要注意两个法向量的夹角不一定是所求的二面角,也可能两个法向量夹角的补角为所求的角,因此要结合实际图形判断所求角是锐角还是钝角。
10. 利用空间向量证明线面平行方法有:
①证明直线的方向向量与平面的某一法向量垂直;
②证明直线的方向向量与平面内某直线的方向向量共线;
③利用共面向量定理,即证明直线的方向向量与平面内的两个不共线向量是共面向量(要注意强调该直线不在平面内)。
相关思维导图模板

树图思维导图提供 2019北京高考数学试题考场答题技巧 在线思维导图免费制作,点击“编辑”按钮,可对 2019北京高考数学试题考场答题技巧 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:079aa9b2ef758958a57d2bd85e2ddf7b

树图思维导图提供 数学立体几何解题技巧 在线思维导图免费制作,点击“编辑”按钮,可对 数学立体几何解题技巧 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9419219fd2fa841e9f8f9e39b44ba963



















 上海工商
上海工商