高考数学辅导：求空间图形中的角思维导图

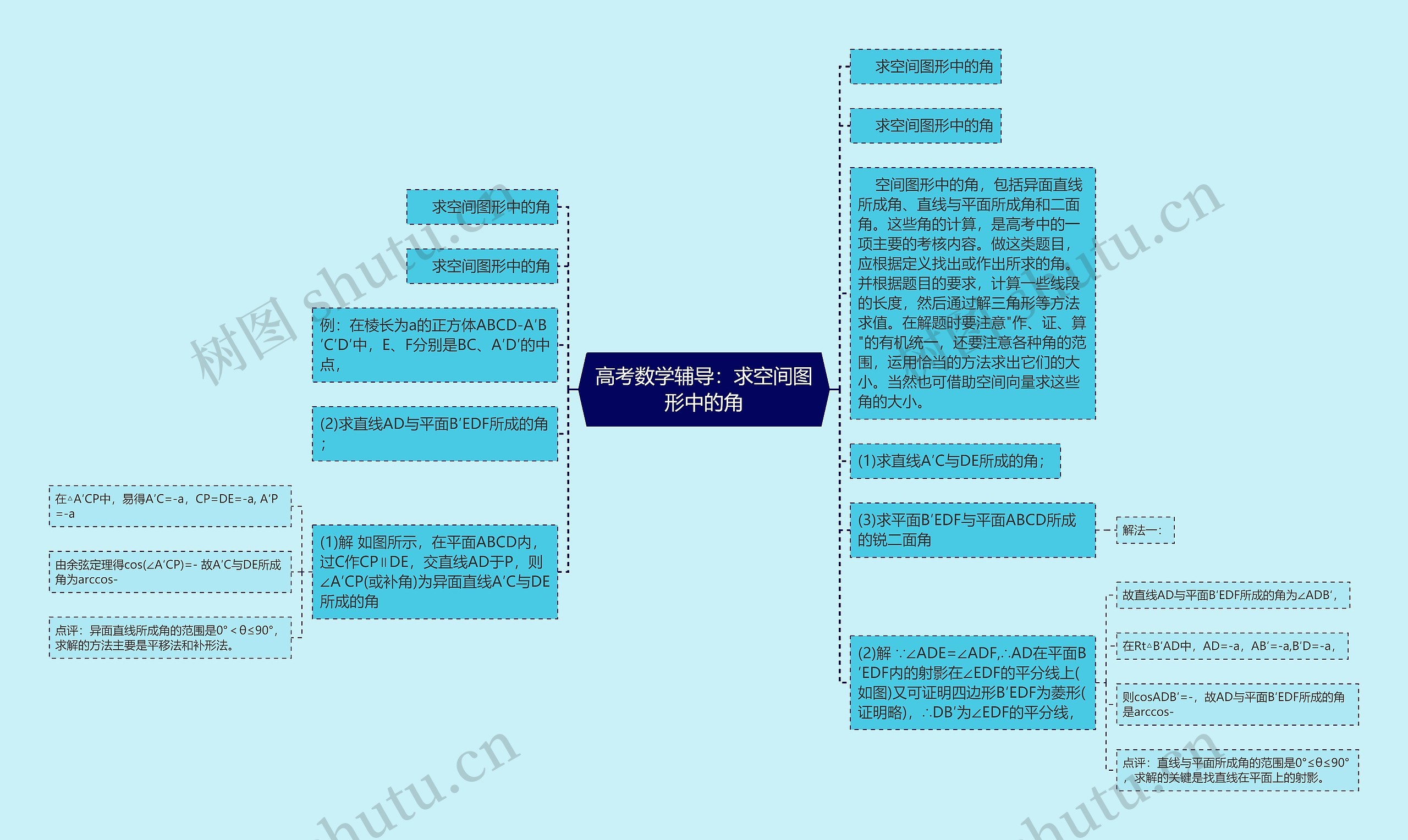
高考数学辅导：求空间图形中的角思维导图，/模板展示了在空间图形中求角的内容，包含异面直线所成角、直线与平面所成角和二面角。这些角的计算是高考中的重要考点，在解题时，需要根据定义找出或作出所求的角，并根据题目要求计算线段的长度，并通过解三角形，解题时需要注意作、证、算的有机统一，要注意不同角的范围，用合适的方法求出他的大小。我们也可以借助空间向量来求解这些角的大小。

举个例子，在一个棱长为a的正方体中，需要求出直线A′C与DE所成的角、直线AD与平面B′EDF所成的角和平面B′EDF与平面ABCD所成的锐二面角。

解法一：

对于直线A′C与DE所成的角，可以通过平移法或补形法来求解。可以在平面ABCD内作一条与DE平行且通过C的直线CP，将其与直线AD的交点记为P，那么∠A′CP就是所求角。

对于直线AD与平面B′EDF所成的角，可以通过找直线AD在平面上的射影来求解。由于∠ADE=∠ADF，所以AD在平面B′EDF内的射影在∠EDF的平分线上，而四边形B′EDF是菱形，所以直线DB′即为∠EDF的平分线，直线AD与平面B′EDF所成的角就是∠ADB′。

对于平面B′EDF与平面ABCD所成的锐二面角，可以通过空间向量的方法来求解。

在解空间图形中的角问题时，需要运用定义、计算线段长度和解三角形，并要注意角的范围和使用合适的求解方法。