高考数学复习:不等式专题热点问题思维导图
高考数学复习:不等式专题热点问题思维导图包含不等式的性质、均值不等式与解不等式,在解决性质问题时,第1.2题往往忽略,均值不等式容易出错的地方集中第3.4两题上和第2题选项C,线性规划部分选择了约束条件或目标函数中含有参数的题目,在思考方法上,第2.3.4题要掌握最值出现边界点上的基本原则,第5.6题通过图形和动态的观点揭示题目的立意。第7题包含量的“转换”,第8.9题则是应用题,具体的知识点包含不等式的性质、均值不等式与解不等式的推导和应用,和如何处理约束条件和目标函数中含有参数的题目。
思维导图大纲
高考数学复习:不等式专题热点问题思维导图模板大纲
天津市第四十二中学 张鼎言
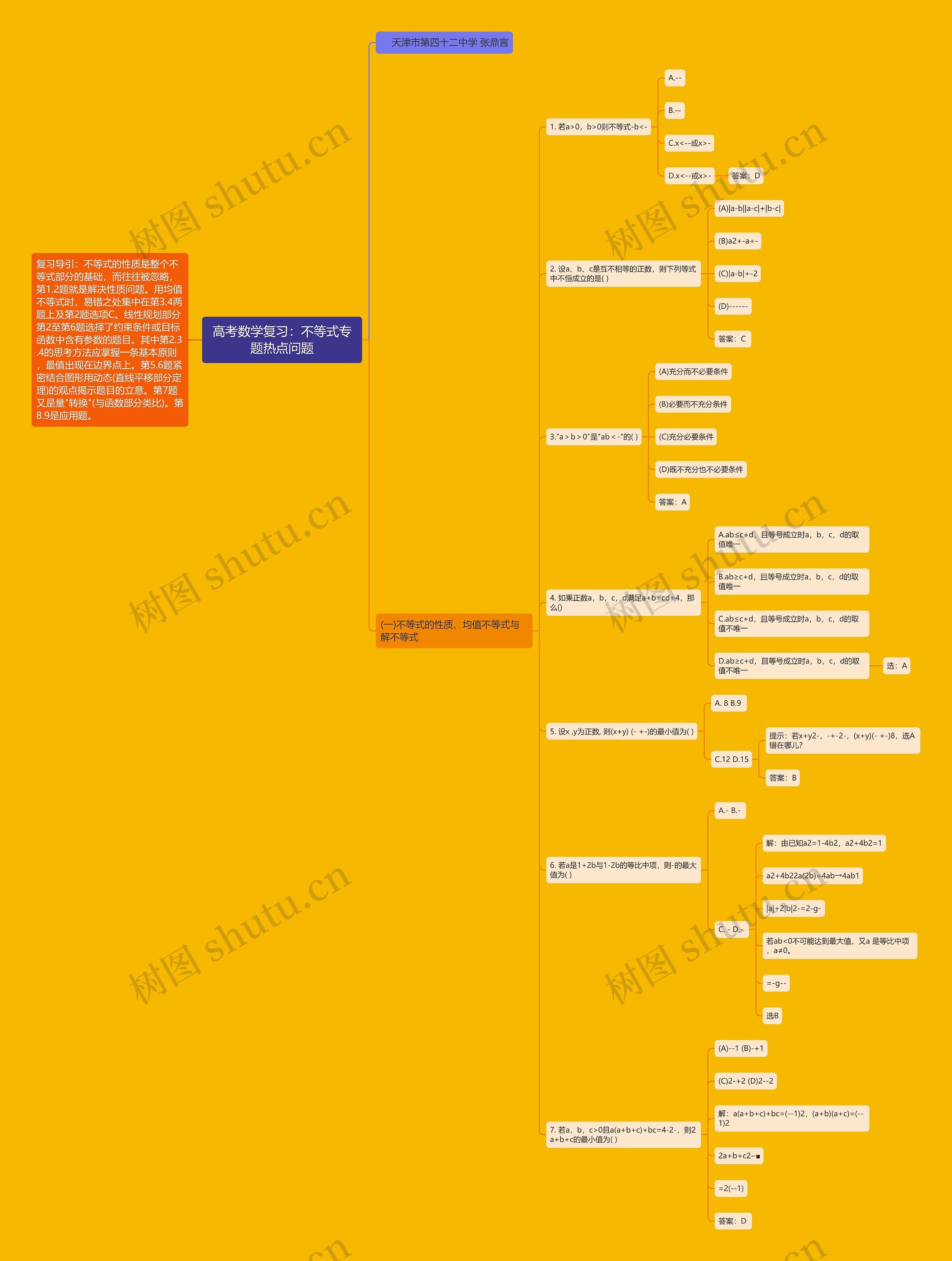
复习导引:不等式的性质是整个不等式部分的基础,而往往被忽略,第1.2题就是解决性质问题。用均值不等式时,易错之处集中在第3.4两题上及第2题选项C。线性规划部分第2至第6题选择了约束条件或目标函数中含有参数的题目。其中第2.3.4的思考方法应掌握一条基本原则,最值出现在边界点上。第5.6题紧密结合图形用动态(直线平移部分定理)的观点揭示题目的立意。第7题又是量"转换"(与函数部分类比)。第8.9是应用题。
(一)不等式的性质、均值不等式与解不等式
1. 若a>0,b>0则不等式-b<-
A.--
B.--
C.x<--或x>-
D.x<--或x>-
答案:D
2. 设a、b、c是互不相等的正数,则下列等式中不恒成立的是( )
(A)|a-b||a-c|+|b-c|
(B)a2+-a+-
(C)|a-b|+-2
(D)------
答案:C
3."a>b>0"是"ab<-"的( )
(A)充分而不必要条件
(B)必要而不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
答案:A
4. 如果正数a,b,c,d满足a+b=cd=4,那么()
A.ab≤c+d,且等号成立时a,b,c,d的取值唯一
B.ab≥c+d,且等号成立时a,b,c,d的取值唯一
C.ab≤c+d,且等号成立时a,b,c,d的取值不唯一
D.ab≥c+d,且等号成立时a,b,c,d的取值不唯一
选:A
5. 设x ,y为正数, 则(x+y) (- +-)的最小值为( )
A. 8 B.9
C.12 D.15
提示:若x+y2-,-+-2-,(x+y)(- +-)8,选A错在哪儿?
答案:B
6. 若a是1+2b与1-2b的等比中项,则-的最大值为( )
A.- B.-
C. - D.-
解:由已知a2=1-4b2,a2+4b2=1
a2+4b22a(2b)=4ab→4ab1
|a|+2|b|2-=2-g-
若ab<0不可能达到最大值,又a 是等比中项,a≠0。
=-g--
选B
7. 若a,b,c>0且a(a+b+c)+bc=4-2-,则2a+b+c的最小值为( )
(A)--1 (B)-+1
(C)2-+2 (D)2--2
解:a(a+b+c)+bc=(--1)2,(a+b)(a+c)=(--1)2
2a+b+c2-·■
=2(--1)
答案:D
相关思维导图模板

树图思维导图提供 数学高考复习计划 在线思维导图免费制作,点击“编辑”按钮,可对 数学高考复习计划 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:406fcead444c261a0e76a864012e2078

树图思维导图提供 高考数学第二轮复习方法 在线思维导图免费制作,点击“编辑”按钮,可对 高考数学第二轮复习方法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:340f4dd28c1e2c228ed15c11da1e88e7













 上海工商
上海工商