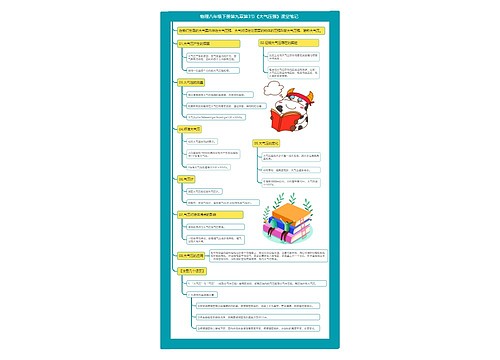
alevel物理-匀加速运动知识点思维导图

1the basic definitions of speed, velocity and acceleration2 the use of the equations of motion for uniform acceleration3 the application of the equations of motion to projectile motion
树图思维导图提供 alevel物理-匀加速运动知识点 在线思维导图免费制作,点击“编辑”按钮,可对 alevel物理-匀加速运动知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7a8fdbe170de6a527ad509696b176560
思维导图大纲
alevel物理-匀加速运动知识点思维导图模板大纲
This Factsheet will cover:
1the basic definitions of speed, velocity and acceleration
2 the use of the equations of motion for uniform acceleration
3 the application of the equations of motion to projectile motion
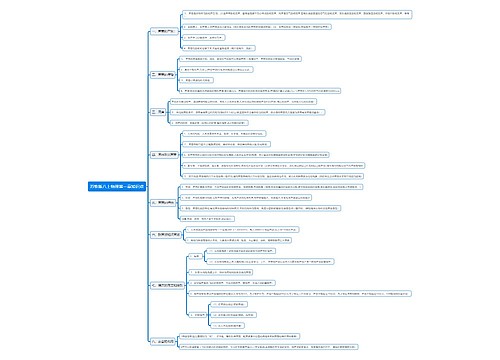
Speed and velocity. Speed is the rate of change of distance.
The speed of a body at any instant is equal to the magnitude of itsvelocity at that instant. However, this is not generally the case foraverage speed and average velocity. To see why this is, imagine walking 5 m North in 2 s, then 5 m South in 2 s. Since you end up at the point where you started, your overall
displacement is zero – so your average velocity is zero. However, you have travelled a distance of 10 m in 4 s, so your average speed is: 10 /4 = 2.5 ms-1.
The average speed will only be the magnitude of the average velocity ifthe body concerned is moving in a straight line, without reversing itsdirection – since then, the distance it moves will always be equal to themagnitude of its displacement.
v = u + atu = initial velocity
v2 = u2 + 2as v = final velocity
s = ut + ½at2 a = acceleration
s = ½ (u + v)t s = displacement from the starting point
t = time
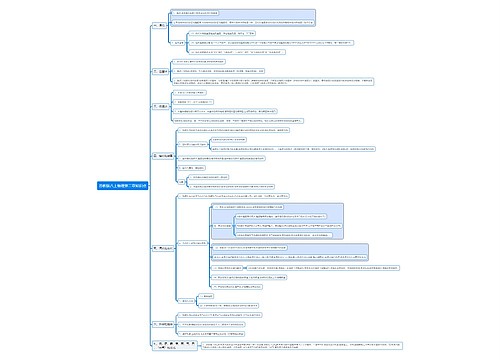
1. Check that the body is moving with constant acceleration!
2. Write down any of u, v, a, s, t that you know
3. Note down which of u, v, a, s and t that you want (e.g. write a = ?)
4. Decide which equation to use by looking at which of the variablesyou have got written down in steps 2 and 3. For example, if youhave got values for u, t and s, and you want a value for v, then youlook for the equation with u, t, s and v in it.
5. Substitute the values you know in, then rearrange.
6. Check that the answer makes sense.
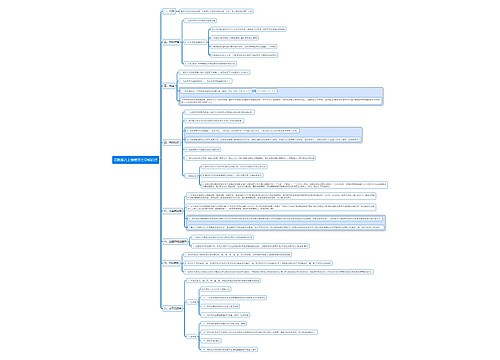
Typical example of Motion
A particle is moving in a straight line with constant acceleration. It passes point P with speed 2 ms-1. Ten seconds later, it passes point Q. The distance between P and Q is 40 metres. Find the speed of the particle as it passes point Q.
We know: u = 2ms-1 s = 40 m t = 10 s
We want: v = ?
Since we have u, s, t and v involved, use s = ½ (u + v)t
Substituting in:
40 = ½ (2 + v)10
40 = 5(2 + v)
40 = 10 + 5v
30 = 5v
v = 6 ms-1
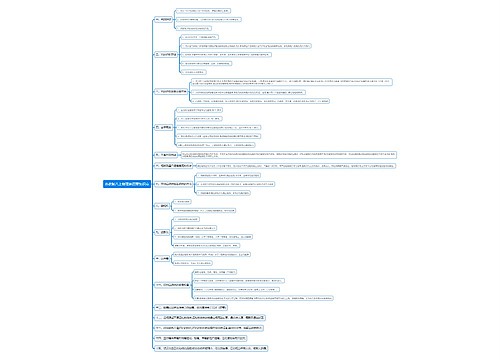
A particle is moving in a straight line with constant acceleration 0.2 ms-2. After it has moved a total of 20m, its speed is 8ms-1. Find its initial speed
a = 0.2 ms-2 s = 20m v = 8 ms-1 u = ?
So use v2 = u2 + 2as
82 = u2 + 2(0.2)(20)
64 = u2 + 8
56 = u2
u = 7.48 ms-1 (3SF)
1. It is usually easier to put the values in before rearranging theequations.
2. Take particular care with negative values. On manycalculators, if you type in –22, you will get the answer –4,rather than the correct value of 4. This is because thecalculator squares before "noticing" the minus sign.
















 上海工商
上海工商