单调队列思维导图
单调队列知识梳理
树图思维导图提供 单调队列 在线思维导图免费制作,点击“编辑”按钮,可对 单调队列 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:2192b98136a365d9abec76d523968818
思维导图大纲
单调队列思维导图模板大纲
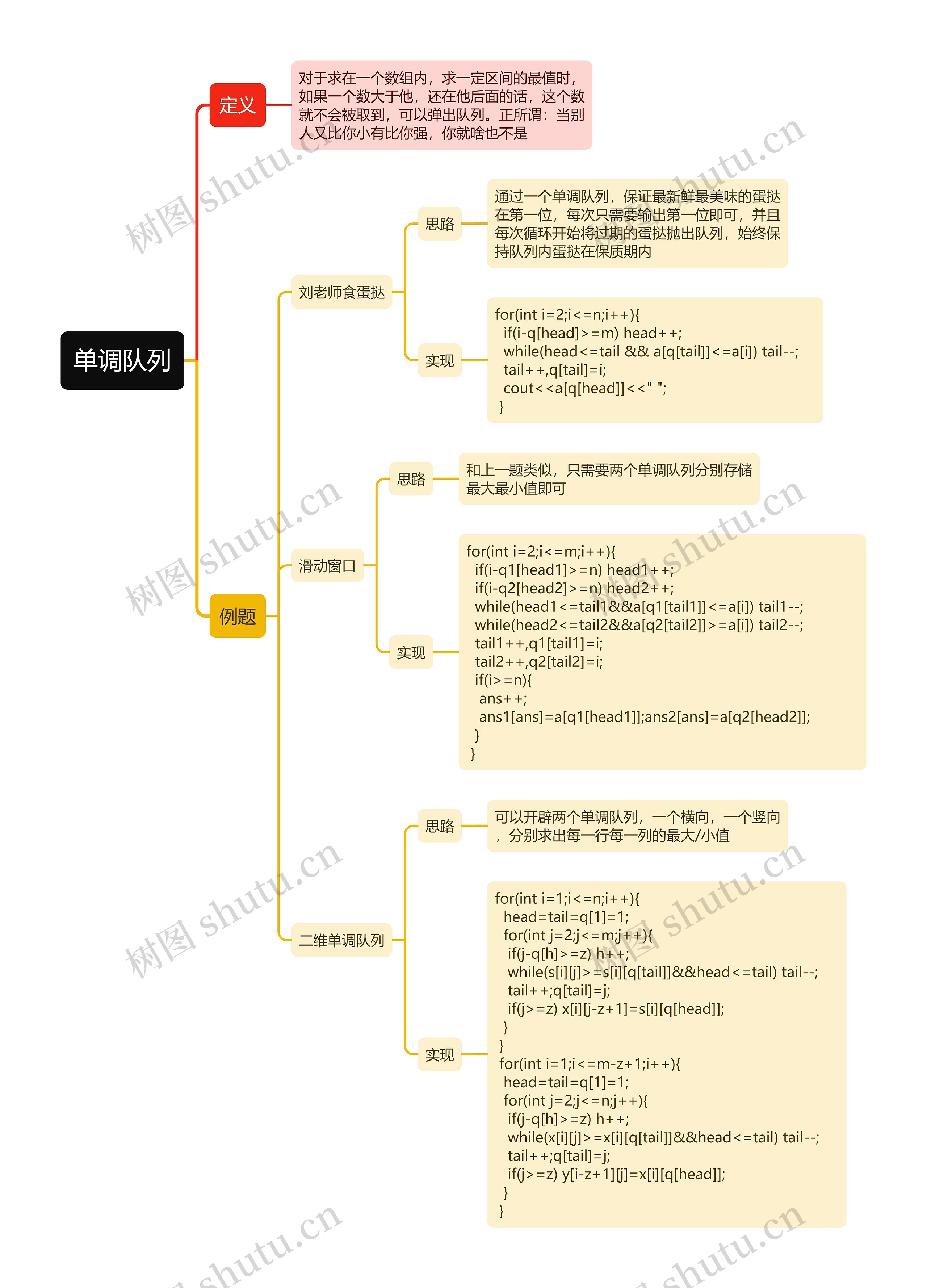
定义
对于求在一个数组内,求一定区间的最值时, 如果一个数大于他,还在他后面的话,这个数 就不会被取到,可以弹出队列。正所谓:当别人又比你小有比你强,你就啥也不是
例题
刘老师食蛋挞
思路
通过一个单调队列,保证最新鲜最美味的蛋挞 在第一位,每次只需要输出第一位即可,并且每次循环开始将过期的蛋挞抛出队列,始终保持队列内蛋挞在保质期内
实现
for(int i=2;i<=n;i++){ if(i-q[head]>=m) head++; while(head<=tail && a[q[tail]]<=a[i]) tail--; tail++,q[tail]=i; cout<<a[q[head]]<<" "; }
滑动窗口
思路
和上一题类似,只需要两个单调队列分别存储最大最小值即可
实现
for(int i=2;i<=m;i++){ if(i-q1[head1]>=n) head1++; if(i-q2[head2]>=n) head2++; while(head1<=tail1&&a[q1[tail1]]<=a[i]) tail1--; while(head2<=tail2&&a[q2[tail2]]>=a[i]) tail2--; tail1++,q1[tail1]=i; tail2++,q2[tail2]=i; if(i>=n){ ans++; ans1[ans]=a[q1[head1]];ans2[ans]=a[q2[head2]]; } }
二维单调队列
思路
可以开辟两个单调队列,一个横向,一个竖向,分别求出每一行每一列的最大/小值
实现
for(int i=1;i<=n;i++){ head=tail=q[1]=1; for(int j=2;j<=m;j++){ if(j-q[h]>=z) h++; while(s[i][j]>=s[i][q[tail]]&&head<=tail) tail--; tail++;q[tail]=j; if(j>=z) x[i][j-z+1]=s[i][q[head]]; } } for(int i=1;i<=m-z+1;i++){ head=tail=q[1]=1; for(int j=2;j<=n;j++){ if(j-q[h]>=z) h++; while(x[i][j]>=x[i][q[tail]]&&head<=tail) tail--; tail++;q[tail]=j; if(j>=z) y[i-z+1][j]=x[i][q[head]]; } }
相关思维导图模板


树图思维导图提供 环境空气污染和胰岛素敏感性之间的纵向关联:来自KORA队列研究的结果 在线思维导图免费制作,点击“编辑”按钮,可对 环境空气污染和胰岛素敏感性之间的纵向关联:来自KORA队列研究的结果 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:05a1570de9aff1ce3943db94321ac5c5

树图思维导图提供 长期暴露于低水平的环境空气污染和中风和冠心病的发病率:在过去的项目内,对6个欧洲队列的汇总分析 在线思维导图免费制作,点击“编辑”按钮,可对 长期暴露于低水平的环境空气污染和中风和冠心病的发病率:在过去的项目内,对6个欧洲队列的汇总分析 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:aeb214df5055d8c5f449655fbfd81f7d
















 上海工商
上海工商