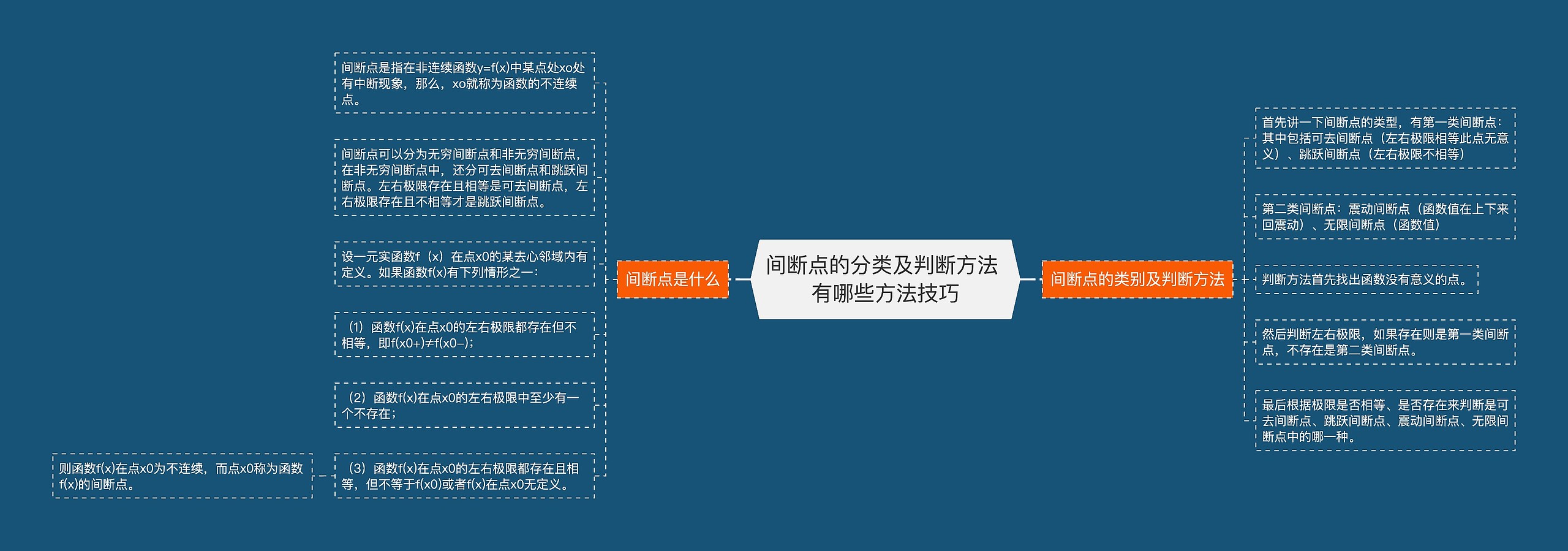
间断点的分类及判断方法 有哪些方法技巧思维导图
如果函数f在点x连续,则称x是函数f的连续点;如果函数f在点x不连续,则称x是函数f的间断点。
树图思维导图提供 间断点的分类及判断方法 有哪些方法技巧 在线思维导图免费制作,点击“编辑”按钮,可对 间断点的分类及判断方法 有哪些方法技巧 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:e0350cb528d974983465bd74c803af6d
思维导图大纲
间断点的分类及判断方法 有哪些方法技巧思维导图模板大纲
间断点的类别及判断方法
首先讲一下间断点的类型,有第一类间断点:其中包括可去间断点(左右极限相等此点无意义)、跳跃间断点(左右极限不相等)
第二类间断点:震动间断点(函数值在上下来回震动)、无限间断点(函数值)
判断方法首先找出函数没有意义的点。
然后判断左右极限,如果存在则是第一类间断点,不存在是第二类间断点。
最后根据极限是否相等、是否存在来判断是可去间断点、跳跃间断点、震动间断点、无限间断点中的哪一种。
间断点是什么
间断点是指在非连续函数y=f(x)中某点处xo处有中断现象,那么,xo就称为函数的不连续点。
间断点可以分为无穷间断点和非无穷间断点,在非无穷间断点中,还分可去间断点和跳跃间断点。左右极限存在且相等是可去间断点,左右极限存在且不相等才是跳跃间断点。
设一元实函数f(x)在点x0的某去心邻域内有定义。如果函数f(x)有下列情形之一:
(1)函数f(x)在点x0的左右极限都存在但不相等,即f(x0+)≠f(x0-);
(2)函数f(x)在点x0的左右极限中至少有一个不存在;
(3)函数f(x)在点x0的左右极限都存在且相等,但不等于f(x0)或者f(x)在点x0无定义。
则函数f(x)在点x0为不连续,而点x0称为函数f(x)的间断点。
相关思维导图模板
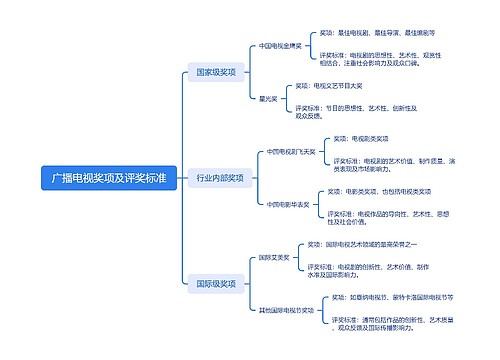

树图思维导图提供 广播电视奖项及评奖标准 在线思维导图免费制作,点击“编辑”按钮,可对 广播电视奖项及评奖标准 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a4210651fa3a78355ac9f5101bb2c616


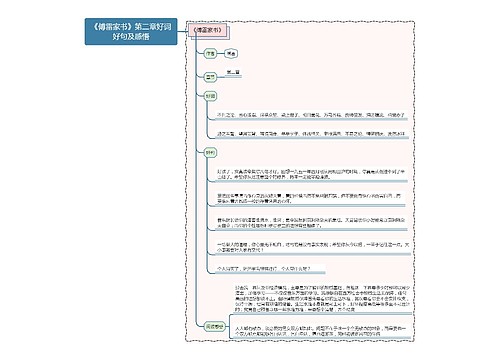
树图思维导图提供 抓住重点 在线思维导图免费制作,点击“编辑”按钮,可对 抓住重点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4c49e4799ddf94a339c56e46eb96a826











 上海工商
上海工商