等差数列求和公式 推导方法有哪些思维导图
等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列。那么,等差数列求和公式有哪些呢?下面小编整理了一些相关信息,供大家参考!
树图思维导图提供 等差数列求和公式 推导方法有哪些 在线思维导图免费制作,点击“编辑”按钮,可对 等差数列求和公式 推导方法有哪些 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:910afb749edaa6fb35054fc28217f72d
思维导图大纲
等差数列求和公式 推导方法有哪些思维导图模板大纲
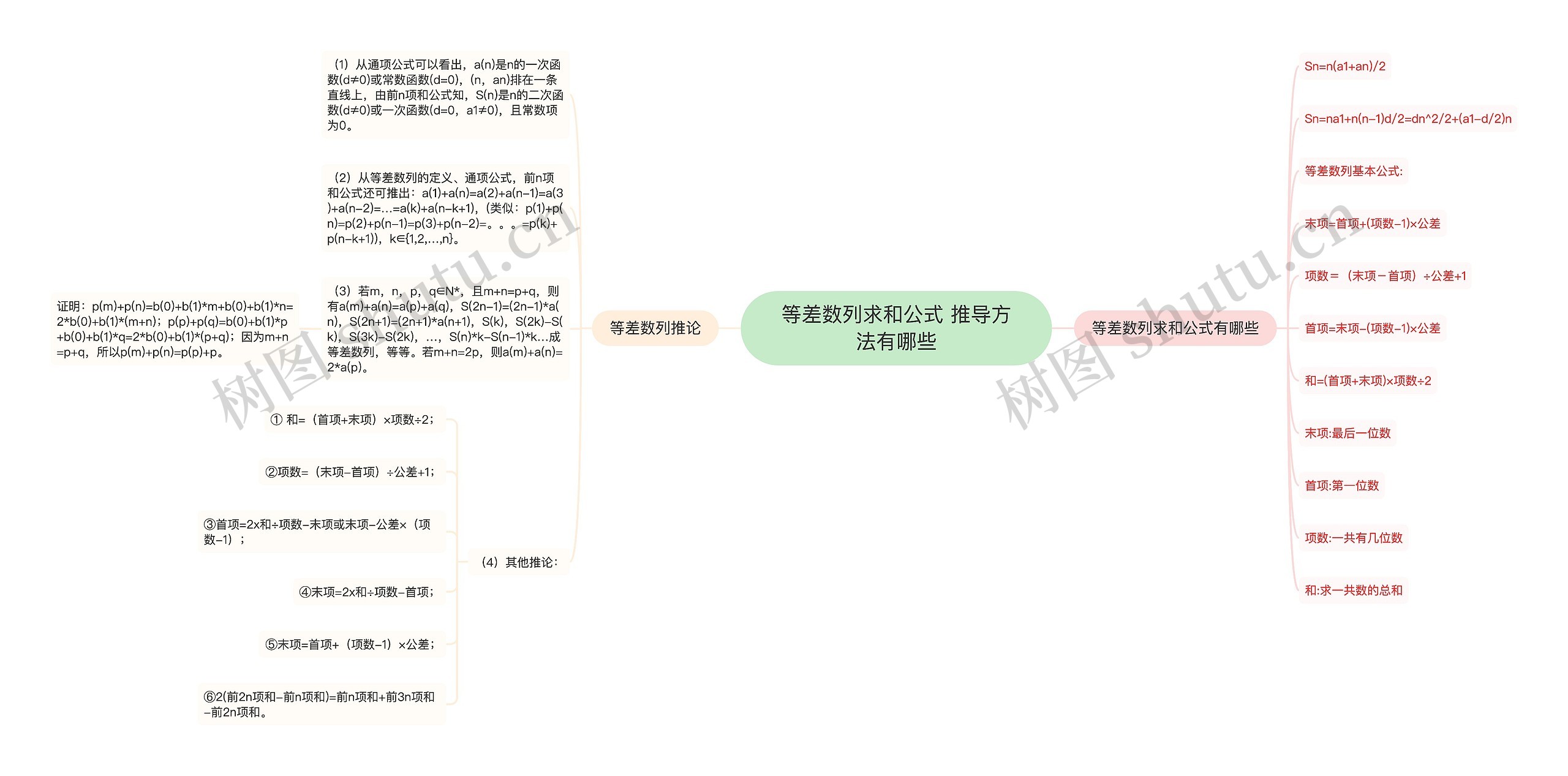
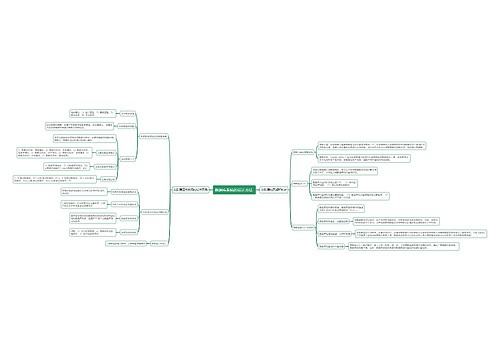
等差数列求和公式有哪些
Sn=n(a1+an)/2
Sn=na1+n(n-1)d/2=dn^2/2+(a1-d/2)n
等差数列基本公式:
末项=首项+(项数-1)×公差
项数=(末项-首项)÷公差+1
首项=末项-(项数-1)×公差
和=(首项+末项)×项数÷2
末项:最后一位数
首项:第一位数
项数:一共有几位数
和:求一共数的总和
等差数列推论
(1)从通项公式可以看出,a(n)是n的一次函数(d≠0)或常数函数(d=0),(n,an)排在一条直线上,由前n项和公式知,S(n)是n的二次函数(d≠0)或一次函数(d=0,a1≠0),且常数项为0。
(2)从等差数列的定义、通项公式,前n项和公式还可推出:a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=…=a(k)+a(n-k+1),(类似:p(1)+p(n)=p(2)+p(n-1)=p(3)+p(n-2)=。。。=p(k)+p(n-k+1)),k∈{1,2,…,n}。
(3)若m,n,p,q∈N*,且m+n=p+q,则有a(m)+a(n)=a(p)+a(q),S(2n-1)=(2n-1)*a(n),S(2n+1)=(2n+1)*a(n+1),S(k),S(2k)-S(k),S(3k)-S(2k),…,S(n)*k-S(n-1)*k…成等差数列,等等。若m+n=2p,则a(m)+a(n)=2*a(p)。
证明:p(m)+p(n)=b(0)+b(1)*m+b(0)+b(1)*n=2*b(0)+b(1)*(m+n);p(p)+p(q)=b(0)+b(1)*p+b(0)+b(1)*q=2*b(0)+b(1)*(p+q);因为m+n=p+q,所以p(m)+p(n)=p(p)+p。
(4)其他推论:
① 和=(首项+末项)×项数÷2;
②项数=(末项-首项)÷公差+1;
③首项=2x和÷项数-末项或末项-公差×(项数-1);
④末项=2x和÷项数-首项;
⑤末项=首项+(项数-1)×公差;
⑥2(前2n项和-前n项和)=前n项和+前3n项和-前2n项和。
相关思维导图模板


树图思维导图提供 抓住重点 在线思维导图免费制作,点击“编辑”按钮,可对 抓住重点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4c49e4799ddf94a339c56e46eb96a826

树图思维导图提供 乌审旗国有投资集团有限公司 在线思维导图免费制作,点击“编辑”按钮,可对 乌审旗国有投资集团有限公司 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:5a28142386bd70b085d0dfa0b38ffb1d










 上海工商
上海工商