狭义相对论力学基础-大学物理知识点思维导图
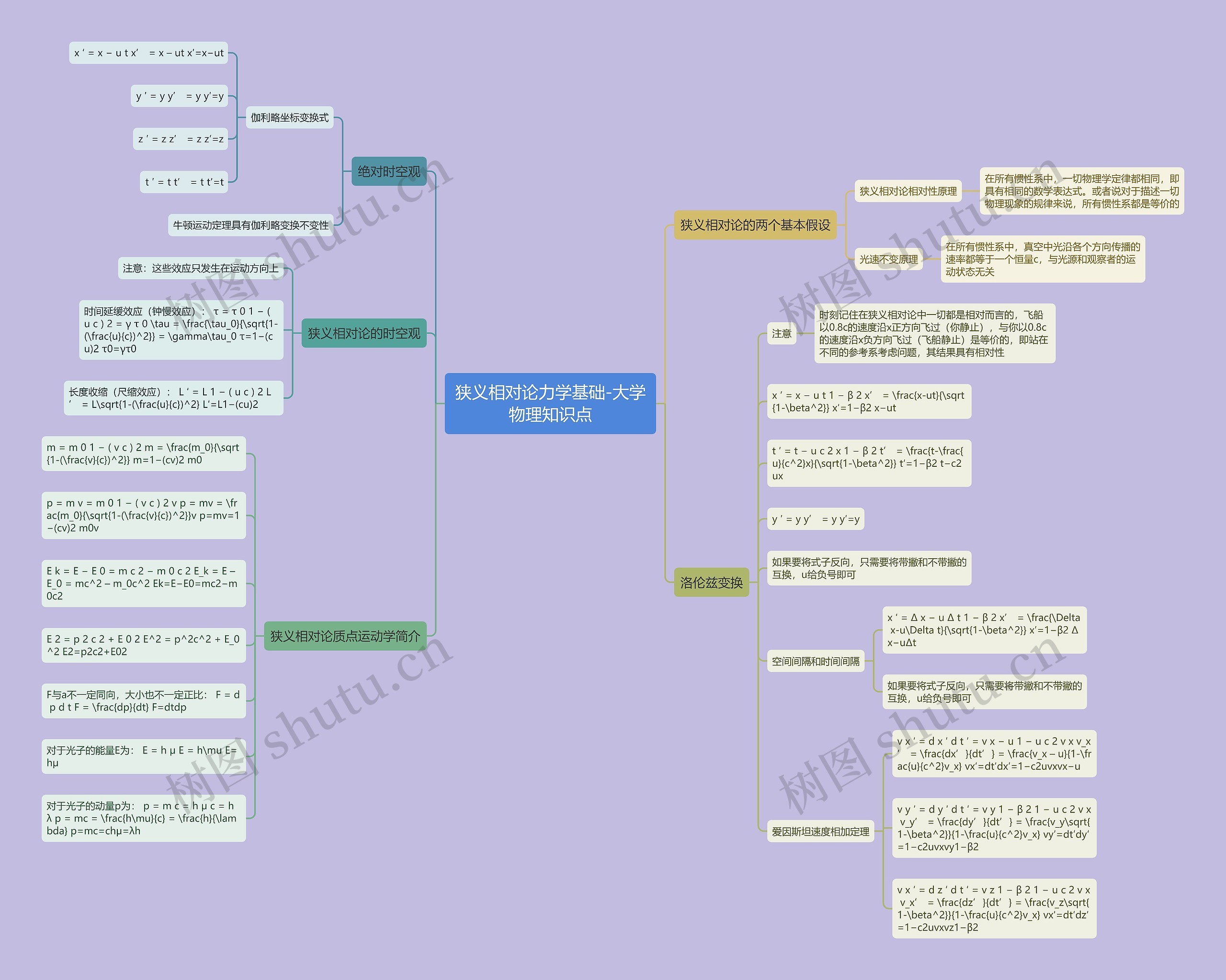
狭义相对论力学基础-大学物理知识点;绝对时空观、狭义相对论的两个基本假设、洛伦兹变换、狭义相对论的时空观、狭义相对论质点运动学简介
树图思维导图提供 狭义相对论力学基础-大学物理知识点 在线思维导图免费制作,点击“编辑”按钮,可对 狭义相对论力学基础-大学物理知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f60dd2b62b1e66a982d092c9c3ee9154
思维导图大纲
狭义相对论力学基础-大学物理知识点思维导图模板大纲
绝对时空观
伽利略坐标变换式
x ′ = x − u t x’ = x – ut x′=x−ut
y ′ = y y’ = y y′=y
z ′ = z z’ = z z′=z
t ′ = t t’ = t t′=t
牛顿运动定理具有伽利略变换不变性
狭义相对论的两个基本假设
狭义相对论相对性原理
在所有惯性系中,一切物理学定律都相同,即具有相同的数学表达式。或者说对于描述一切物理现象的规律来说,所有惯性系都是等价的
光速不变原理
在所有惯性系中,真空中光沿各个方向传播的速率都等于一个恒量c,与光源和观察者的运动状态无关
狭义相对论的时空观
注意:这些效应只发生在运动方向上
时间延缓效应(钟慢效应): τ = τ 0 1 − ( u c ) 2 = γ τ 0 \tau = \frac{\tau_0}{\sqrt{1-(\frac{u}{c})^2}} = \gamma\tau_0 τ=1−(cu)2 τ0=γτ0
长度收缩(尺缩效应): L ′ = L 1 − ( u c ) 2 L’ = L\sqrt{1-(\frac{u}{c})^2} L′=L1−(cu)2
洛伦兹变换
注意
时刻记住在狭义相对论中一切都是相对而言的,飞船以0.8c的速度沿x正方向飞过(你静止),与你以0.8c的速度沿x负方向飞过(飞船静止)是等价的,即站在不同的参考系考虑问题,其结果具有相对性
x ′ = x − u t 1 − β 2 x’ = \frac{x-ut}{\sqrt{1-\beta^2}} x′=1−β2 x−ut
t ′ = t − u c 2 x 1 − β 2 t’ = \frac{t-\frac{u}{c^2}x}{\sqrt{1-\beta^2}} t′=1−β2 t−c2ux
y ′ = y y’ = y y′=y
如果要将式子反向,只需要将带撇和不带撇的互换,u给负号即可
空间间隔和时间间隔
x ′ = Δ x − u Δ t 1 − β 2 x’ = \frac{\Delta x-u\Delta t}{\sqrt{1-\beta^2}} x′=1−β2 Δx−uΔt
如果要将式子反向,只需要将带撇和不带撇的互换,u给负号即可
爱因斯坦速度相加定理
v x ′ = d x ′ d t ′ = v x − u 1 − u c 2 v x v_x’ = \frac{dx’}{dt’} = \frac{v_x – u}{1-\frac{u}{c^2}v_x} vx′=dt′dx′=1−c2uvxvx−u
v y ′ = d y ′ d t ′ = v y 1 − β 2 1 − u c 2 v x v_y’ = \frac{dy’}{dt’} = \frac{v_y\sqrt{1-\beta^2}}{1-\frac{u}{c^2}v_x} vy′=dt′dy′=1−c2uvxvy1−β2
v x ′ = d z ′ d t ′ = v z 1 − β 2 1 − u c 2 v x v_x’ = \frac{dz’}{dt’} = \frac{v_z\sqrt{1-\beta^2}}{1-\frac{u}{c^2}v_x} vx′=dt′dz′=1−c2uvxvz1−β2
狭义相对论质点运动学简介
m = m 0 1 − ( v c ) 2 m = \frac{m_0}{\sqrt{1-(\frac{v}{c})^2}} m=1−(cv)2 m0
p = m v = m 0 1 − ( v c ) 2 v p = mv = \frac{m_0}{\sqrt{1-(\frac{v}{c})^2}}v p=mv=1−(cv)2 m0v
E k = E − E 0 = m c 2 − m 0 c 2 E_k = E – E_0 = mc^2 – m_0c^2 Ek=E−E0=mc2−m0c2
E 2 = p 2 c 2 + E 0 2 E^2 = p^2c^2 + E_0^2 E2=p2c2+E02
F与a不一定同向,大小也不一定正比: F = d p d t F = \frac{dp}{dt} F=dtdp
对于光子的能量E为: E = h μ E = h\mu E=hμ
对于光子的动量p为: p = m c = h μ c = h λ p = mc = \frac{h\mu}{c} = \frac{h}{\lambda} p=mc=chμ=λh
相关思维导图模板

树图思维导图提供 Linux 网络基础知识 在线思维导图免费制作,点击“编辑”按钮,可对 Linux 网络基础知识 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:199680f0e48eac8a1aeaadb90447d4f4


树图思维导图提供 抓住重点 在线思维导图免费制作,点击“编辑”按钮,可对 抓住重点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4c49e4799ddf94a339c56e46eb96a826





 上海工商
上海工商