人教版九年级数学上册第二十四章圆思维导图
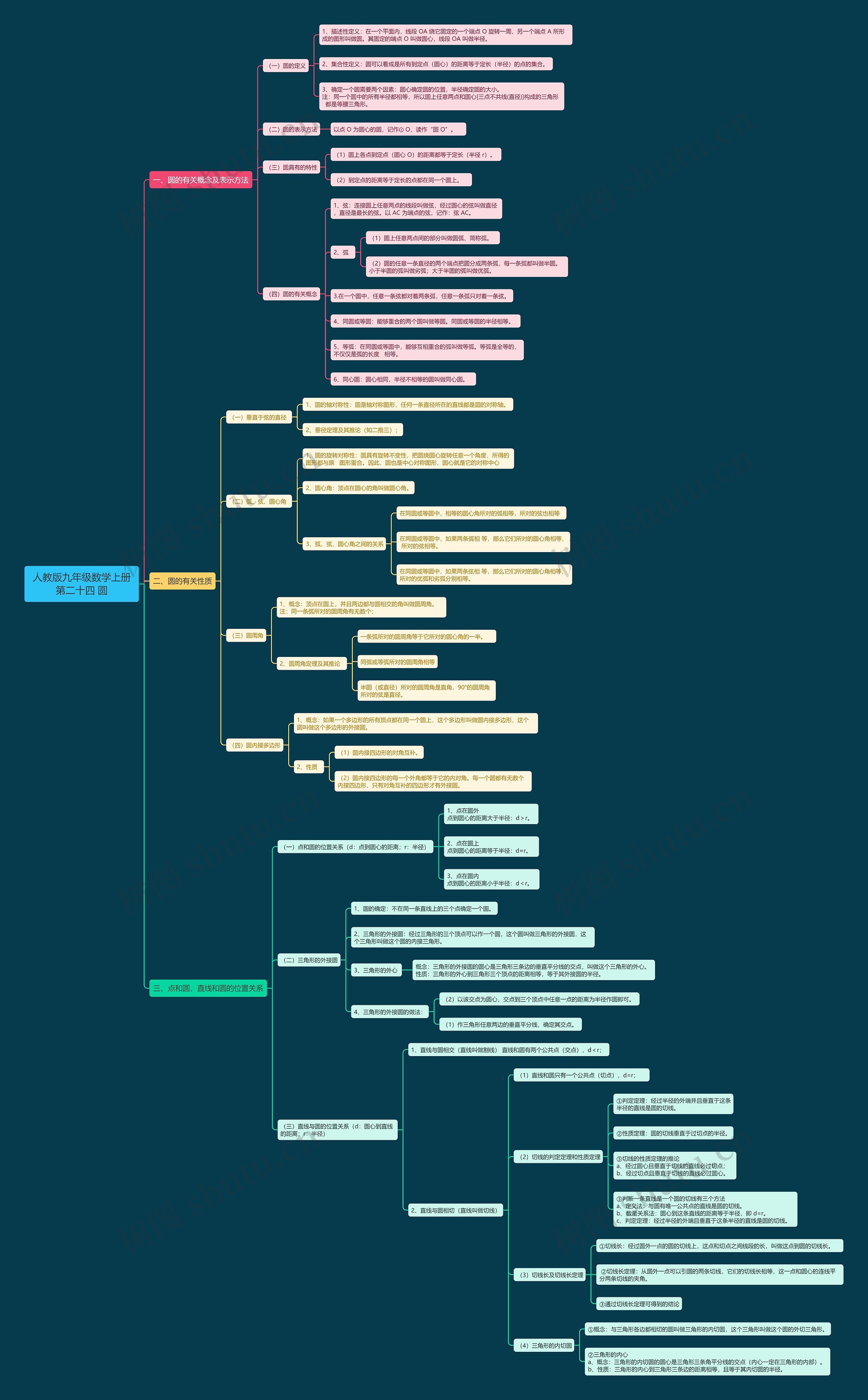
人教版九年级数学上册第二十四章圆思维导图包含到圆的相关知识点,包含圆的定义、表示方法和特性,圆心角、圆周角和弧、弦、圆心角之间的关系,垂径定理推论。圆的定义可以通过描述性定义、集合性定义和半径、圆心的确定进行理解,在圆的表示方法中,以点O为圆心的圆可以记作⨀O,圆/的特性包含任意点到定点(圆心)的距离都等于定长(半径r),和到定点的距离等于定长的点都在同一个圆上。在圆的有关概念中,弦、半圆、劣弧、优弧、同心圆都具有具体定义,圆也具有轴对称性和旋转对称性,对于圆心角、圆周角和弧、弦、圆心角之间的关系,同圆或等圆情况下,相等的圆心角所对的弧相等,所对的弦也相等。在同圆或等圆中,如果两条弧相等,那么他所对的圆心角相等,所对的弦相等,在同圆或等圆中,如果两条弦相等,那么他所对的圆心角相等,所对的优弧和劣弧分别相等,圆周角定理则是指一条弧所对的圆周角等于他所对的圆心角的一半。
思维导图大纲
人教版九年级数学上册第二十四 圆思维导图模板大纲
一、圆的有关概念及表示方法
(一)圆的定义
1、描述性定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形 成的图形叫做圆。其固定的端点 O 叫做圆心,线段 OA 叫做半径。
2、集合性定义:圆可以看成是所有到定点(圆心)的距离等于定长(半径)的点的集合。
3、确定一个圆需要两个因素:圆心确定圆的位置,半径确定圆的大小。 注:同一个圆中的所有半径都相等,所以圆上任意两点和圆心[三点不共线(直径)]构成的三角形 都是等腰三角形。
(二)圆的表示方法
以点 O 为圆心的圆,记作⨀ O,读作“圆 O”。
(三)圆具有的特性
(1)圆上各点到定点(圆心 O)的距离都等于定长(半径 r)。
(2)到定点的距离等于定长的点都在同一个圆上。
(四)圆的有关概念
1、弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径,直径是最长的弦。以 AC 为端点的弦,记作:弦 AC。
2、弧
(1)圆上任意两点间的部分叫做圆弧、简称弧。
(2)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。 小于半圆的弧叫做劣弧;大于半圆的弧叫做优弧。
3.在一个圆中,任意一条弦都对着两条弧,任意一条弧只对着一条弦。
4、同圆或等圆:能够重合的两个圆叫做等圆。同圆或等圆的半径相等。
5、等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。等弧是全等的,不仅仅是弧的长度 相等。
6、同心圆:圆心相同,半径不相等的圆叫做同心圆。
二、圆的有关性质
(一)垂直于弦的直径
1、圆的轴对称性:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴。
2、垂径定理及其推论(知二推三);
(二)弧、弦、圆心角
1、圆的旋转对称性:圆具有旋转不变性,把圆绕圆心旋转任意一个角度,所得的图形都与原 图形重合。因此,圆也是中心对称图形,圆心就是它的对称中心
2、圆心角:顶点在圆心的角叫做圆心角。
3、弧、弦、圆心角之间的关系
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等
在同圆或等圆中,如果两条弧相 等,那么它们所对的圆心角相等, 所对的弦相等。
在同圆或等圆中,如果两条弦相 等,那么它们所对的圆心角相等, 所对的优弧和劣弧分别相等。
(三)圆周角
1、概念:顶点在圆上,并且两边都与圆相交的角叫做圆周角。 注:同一条弧所对的圆周角有无数个;
2、圆周角定理及其推论
一条弧所对的圆周角等于它所对的圆心角的一半。
同弧或等弧所对的圆周角相等
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
(四)圆内接多边形
1、概念:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个 圆叫做这个多边形的外接圆。
2、性质
(1)圆内接四边形的对角互补。
(2)圆内接四边形的每一个外角都等于它的内对角。每一个圆都有无数个内接四边形,只有对角互补的四边形才有外接圆。
三、点和圆、直线和圆的位置关系
(一)点和圆的位置关系(d:点到圆心的距离;r:半径)
1、点在圆外 点到圆心的距离大于半径:d>r。
2、点在圆上 点到圆心的距离等于半径:d=r。
3、点在圆内 点到圆心的距离小于半径:d<r。
(二)三角形的外接圆
1、圆的确定:不在同一条直线上的三个点确定一个圆。
2、三角形的外接圆:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这 个三角形叫做这个圆的内接三角形。
3、三角形的外心
概念:三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心。 性质:三角形的外心到三角形三个顶点的距离相等,等于其外接圆的半径。
4、三角形的外接圆的做法:
(2)以该交点为圆心,交点到三个顶点中任意一点的距离为半径作圆即可。
(1)作三角形任意两边的垂直平分线,确定其交点。
(三)直线与圆的位置关系(d:圆心到直线的距离;r:半径)
1、直线与圆相交(直线叫做割线) 直线和圆有两个公共点(交点),d<r;
2、直线与圆相切(直线叫做切线)
(1)直线和圆只有一个公共点(切点),d=r;
(2)切线的判定定理和性质定理
①判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
②性质定理:圆的切线垂直于过切点的半径。
③切线的性质定理的推论 a、经过圆心且垂直于切线的直线必过切点; b、经过切点且垂直于切线的直线必过圆心。
③判断一条直线是一个圆的切线有三个方法 a、定义法:与圆有唯一公共点的直线是圆的切线。 b、数量关系法:圆心到这条直线的距离等于半径,即 d=r。 c、判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线。
(3)切线长及切线长定理
①切线长:经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长。
②切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平 分两条切线的夹角。
③通过切线长定理可得到的结论
(4)三角形的内切圆
①概念:与三角形各边都相切的圆叫做三角形的内切圆,这个三角形叫做这个圆的外切三角形。
②三角形的内心 a、概念:三角形的内切圆的圆心是三角形三条角平分线的交点(内心一定在三角形的内部)。 b、性质:三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径。
相关思维导图模板

树图思维导图提供 高一第一学期数学教学计划 在线思维导图免费制作,点击“编辑”按钮,可对 高一第一学期数学教学计划 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:b8e08ba67a9a1244a3ebb42aeea69d57


















 上海工商
上海工商