八年级数学全等三角形考点汇总思维导图与例题分析

编辑by脆脆鲨

全等三角形是初二数学的重要章节，它所涉及的题型也是比较多的，同学们在这上面丢分的也情况也时有发生，为此，小编今天和大家分享八下数学【全等三角形】考点汇总，思维导图+例题分析。

一、为什么用思维导图梳理全等三角形的知识点

在梳理全等三角形的相关内容时，一般会用摘录已经注释的方式从上往下依序说明相关知识内容。而利用思维导图工具梳理全等三角形，则可以结合思维导图工具的特点在整体在基础上系统性地梳理全等三角形的相关内容，以便逻辑有序地展开梳理，并呈现各知识点之间的逻辑关系。

  当然了，除了全等三角形的思维导图外，思维导图还可用于其它诸多场景。如读书笔记、个人规划、工作总结、旅行清单等。更多的知识也可以在【树图网-帮助中心-校园教育】中找到哦~

二、如何用思维导图梳理全等三角形

思维导图作为一种以层级特点梳理发散性内容的工具，首先需要确立好梳理内容的“中心主题”，即全等三角形梳理。随后围绕“中心主题”梳理与之相关的“分支内容”，即全等三角形的相关知识点内容。在利用思维导图工具梳理代词时，注意各层级节点之间的的逻辑关系，有序地梳理各节点内容。

小编在此给大家分享关于全等三角形的思维导图，一起来看看吧～

三、如何画全等三角形的思维导图

想要绘制全等三角形思维导图，通常可以使用树图思维导图进行，这是一款适用于电脑端绘图的工具，打开编辑器后将需要梳理的内容填充至节点即可简单制图，同时还带有诸多“节点样式”与“主题风格”功能辅助绘制精美好看的思维导图。是一款简单好用的思维导图绘制工具。下面给大家简单分享用树图思维导图绘制实词思维导图的方法。

（1）首先通过树图思维导图工具【新建文件-选择合适的结构】并进入到对应的编辑页面；

（2）接下来以层层递进的方式将需要梳理的物理知识相关内容呈现至节点。梳理基本内容；

（3）随后还可以利用插入图标、备注、链接、关系线、概要等功能进一步思维导图的内容；

（4）而后还可以试着借助主题、样式、一键美化等相关功能对思维导图进行适当的优化处理；

（5）当物理知识的思维导图绘制完毕后，直接将图示“保存”至账号云端，或“导出”为png、pdf、jpg等格式即可。

四、大纲

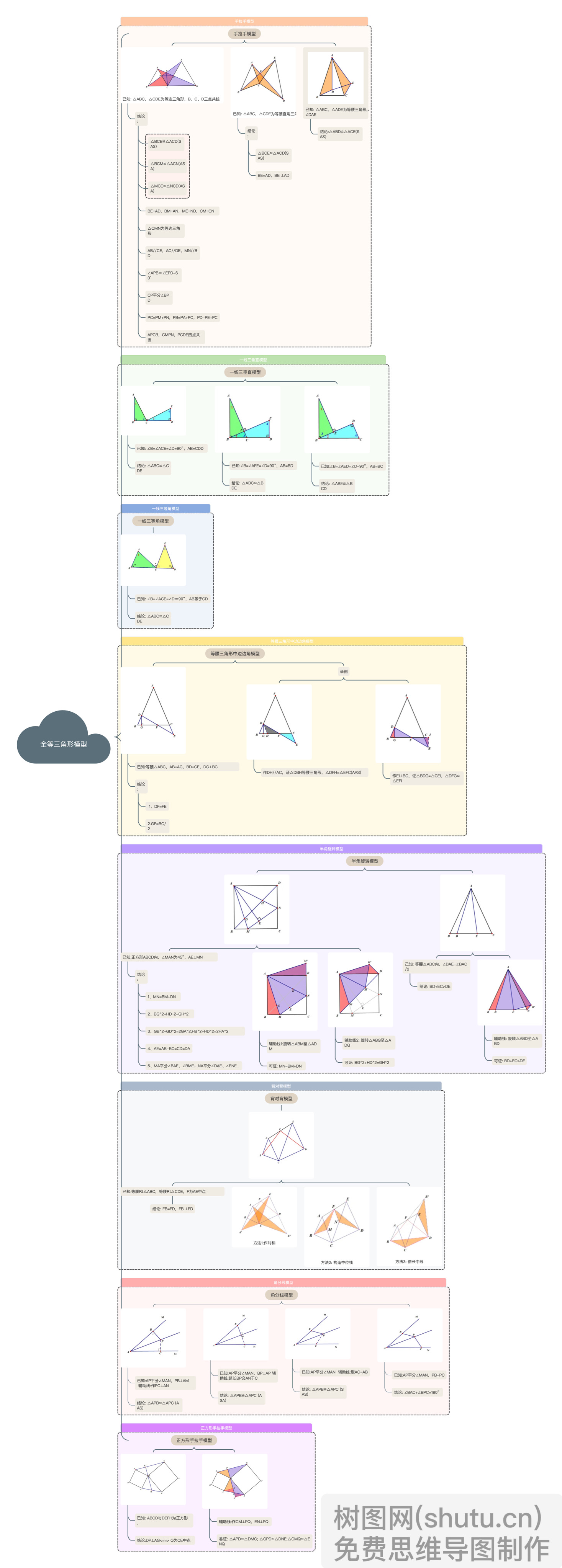
全等三角形模型

手拉手模型

已知: △ABC，△CDE为等边三角形，B、C、D三点共线

结论:

△BCE≌△ACD(SAS)

△BCM≌△ACN(ASA)

△MCE≌△NCD(ASA)

BE=AD，BM=AN，ME=ND，CM=CN

△CMN为等边三角形

AB//CE，AC//DE，MN//BD

∠APB＝∠EPD-60°

CP平分∠BPD

PC=PM+PN，PB=PA+PC，PD-PE+PC

APCB，CMPN，PCDE四点共圈

已知: △ABC，△CDE为等腰直角三角形

结论:

△BCE≌△ACD(SAS)

BE=AD，BE ⊥AD

已知: △ABC，△ADE为等腰三角形,∠BAC=∠DAE

结论:△ABD≌△ACE(SAS)

一线三垂直模型

已知: ∠B=∠ACE=∠D=90”，AB=CDD

结论: △ABC≌△CDE

已知:∠B=∠AFE=∠D=90”，AB=BD

结论: △ABC≌△BDE

已知:∠B=∠AED=∠D-90”，AB=BC

结论: △ABE≌△BCD

一线三等角模型

已知: ∠B=∠ACE=∠D＝90”，AB等于CD

结论: △ABC≌△CDE

等腰三角形中边边角模型

已知:等腰△ABC，AB=AC，BD=CE，DG⊥BC

结论:

 1、DF=FE

2.GF=BC/2

举例

作DH//AC，证△DBH等腰三角形，△DFH=△EFC(AAS)

作EI⊥BC，证△BDG=△CEl，△DFG≌△EFI

半角旋转模型

已知:正方形ABCD内，∠MAN为45”，AE⊥MN

结论:

1、MN=BM+DN

2、BG^2+HD~2=GH^2

3、GB^2+GD^2=2GA^2;HB^2+HD^2=2HA^2

4、AE=AB-BC=CD=DA

5、MA平分∠BAE、∠BME；NA平分∠DAE、∠ENE

辅助线1:旋转△ABM至△ADM

可证: MN=BM+DN

辅助线2: 旋转△ABG至△ADG

可证: BG^2+HD^2=GH^2

己知: 等腰△ABC内，∠DAE=∠BAC/2

结论: BD+EC>DE

辅助线: 旋转△ABD至△ABD

可证: BD+EC>DE

背对背模型

已知:等腰Rt△ABC，等腰Rt△CDE，F为AE中点

结论: FB=FD，FB ⊥FD

方法1:作对称

方法2: 构造中位线

方法3: 倍长中线

角分线模型

已知:AP平分∠MAN，PB⊥AM     辅助线:作PC⊥AN

结论: △APB≌△APC (AAS)

已知:AP平分∠MAN，BP⊥AP 辅助线:延长BP交AN于C

结论: △APB≌△APC (ASA)

已知:AP平分∠MAN  辅助线:取AC=AB

结论: △APB≌△APC (SAS)

已知:AP平分∠MAN，PB=PC

结论: ∠BAC+∠BPC=180”

正方形手拉手模型

已知: ABCD与DEFH为正方形，

结论:DP⊥AG

辅助线:作CM⊥PQ，EN⊥PQ

易证: △APD≌△DMC; △GPD≌△DNE;△CMQ≌△ENQ