一年级数学分解法思维导图
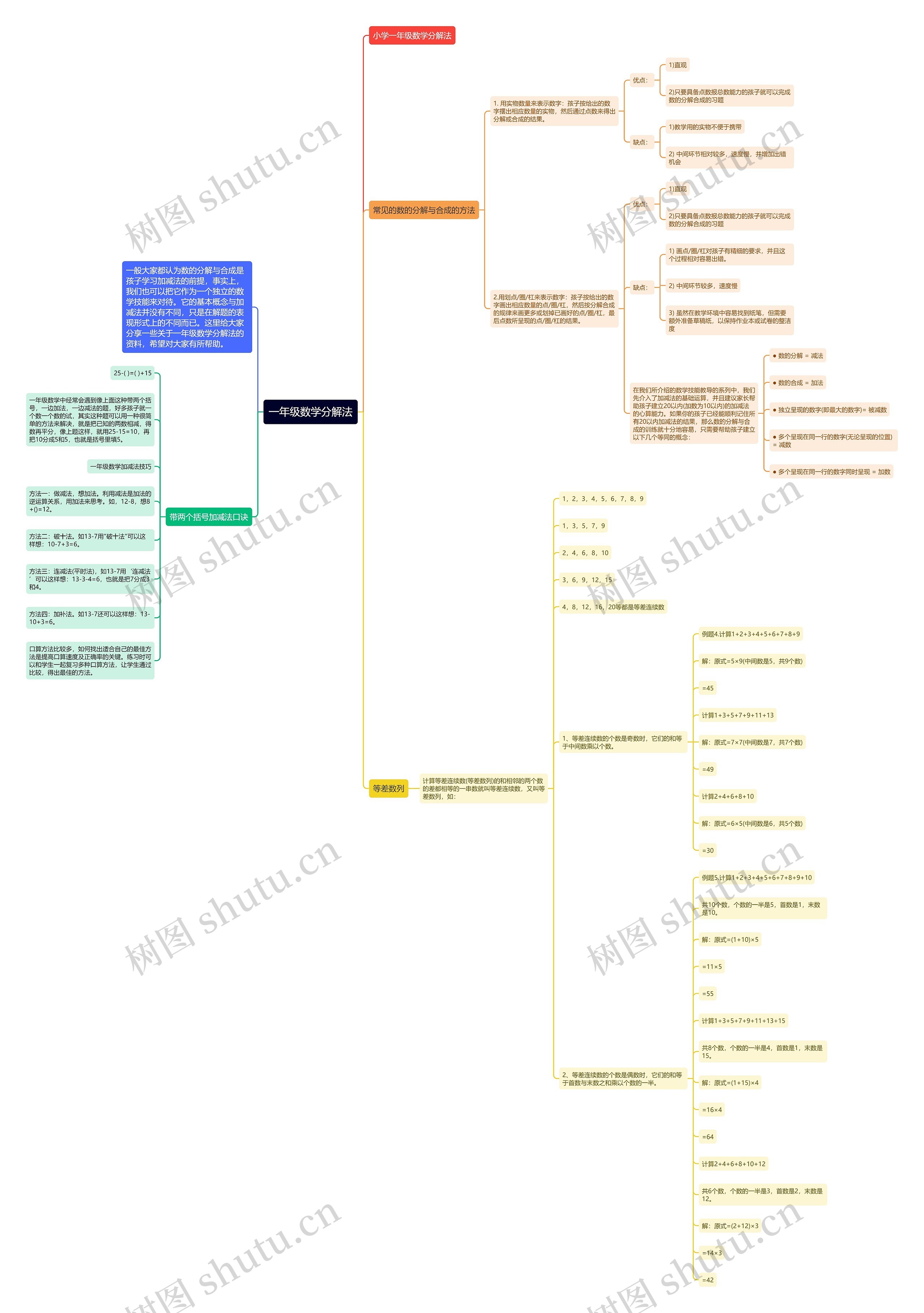
一年级数学分解法思维导图也是一种独立的数学技能,数的分解合成的方法有实物数量表示数字和划点/圈/杠表示数字两种,都直观易学,但也有各自的缺点,建议先让孩子建立20以内的加减法心算能力,在帮助孩子建立数的分解减法和数的合成加法概念,并学会带两个括号加减法口诀,也介绍了一年级数学加减法的三种技巧,即用加法思考减法、破十法和连减法。
思维导图大纲
一年级数学分解法思维导图模板大纲
小学一年级数学分解法
一般大家都认为数的分解与合成是孩子学习加减法的前提,事实上,我们也可以把它作为一个独立的数学技能来对待。它的基本概念与加减法并没有不同,只是在解题的表现形式上的不同而已。这里给大家分享一些关于一年级数学分解法的资料,希望对大家有所帮助。
常见的数的分解与合成的方法
1. 用实物数量来表示数字:孩子按给出的数字摆出相应数量的实物,然后通过点数来得出分解或合成的结果。
优点:
1)直观
2)只要具备点数报总数能力的孩子就可以完成数的分解合成的习题
缺点:
1)教学用的实物不便于携带
2) 中间环节相对较多,速度慢,并增加出错机会
2.用划点/圈/杠来表示数字:孩子按给出的数字画出相应数量的点/圈/杠,然后按分解合成的规律来画更多或划掉已画好的点/圈/杠,最后点数所呈现的点/圈/杠的结果。
优点:
1)直观
2)只要具备点数报总数能力的孩子就可以完成数的分解合成的习题
缺点:
1) 画点/圈/杠对孩子有精细的要求,并且这个过程相对容易出错。
2) 中间环节较多,速度慢
3) 虽然在教学环境中容易找到纸笔,但需要额外准备草稿纸,以保持作业本或试卷的整洁度
在我们所介绍的数学技能教导的系列中,我们先介入了加减法的基础运算,并且建议家长帮助孩子建立20以内(加数为10以内)的加减法的心算能力。如果你的孩子已经能顺利记住所有20以内加减法的结果,那么数的分解与合成的训练就十分地容易,只需要帮助孩子建立以下几个等同的概念:
● 数的分解 = 减法
● 数的合成 = 加法
● 独立呈现的数字(即最大的数字)= 被减数
● 多个呈现在同一行的数字(无论呈现的位置)= 减数
● 多个呈现在同一行的数字同时呈现 = 加数
带两个括号加减法口诀
25-( )=( )+15
一年级数学中经常会遇到像上面这种带两个括号,一边加法,一边减法的题,好多孩子就一个数一个数的试,其实这种题可以用一种很简单的方法来解决,就是把已知的两数相减,得数再平分,像上题这样,就用25-15=10,再把10分成5和5,也就是括号里填5。
一年级数学加减法技巧
方法一:做减法,想加法。利用减法是加法的逆运算关系,用加法来思考。如,12-8,想8+()=12。
方法二:破十法。如13-7用"破十法"可以这样想:10-7+3=6。
方法三:连减法(平时法),如13-7用‘连减法’可以这样想:13-3-4=6,也就是把7分成3和4。
方法四:加补法。如13-7还可以这样想:13-10+3=6。
口算方法比较多,如何找出适合自己的最佳方法是提高口算速度及正确率的关键。练习时可以和学生一起复习多种口算方法,让学生通过比较,得出最佳的方法。
等差数列
计算等差连续数(等差数列)的和相邻的两个数的差都相等的一串数就叫等差连续数,又叫等差数列,如:
1,2,3,4,5,6,7,8,9
1,3,5,7,9
2,4,6,8,10
3,6,9,12,15
4,8,12,16,20等都是等差连续数
1、等差连续数的个数是奇数时,它们的和等于中间数乘以个数。
例题4.计算1+2+3+4+5+6+7+8+9
解:原式=5×9(中间数是5,共9个数)
=45
计算1+3+5+7+9+11+13
解:原式=7×7(中间数是7,共7个数)
=49
计算2+4+6+8+10
解:原式=6×5(中间数是6,共5个数)
=30
2、等差连续数的个数是偶数时,它们的和等于首数与末数之和乘以个数的一半。
例题5.计算1+2+3+4+5+6+7+8+9+10
共10个数,个数的一半是5,首数是1,末数是10。
解:原式=(1+10)×5
=11×5
=55
计算1+3+5+7+9+11+13+15
共8个数,个数的一半是4,首数是1,末数是15。
解:原式=(1+15)×4
=16×4
=64
计算2+4+6+8+10+12
共6个数,个数的一半是3,首数是2,末数是12。
解:原式=(2+12)×3
=14×3
=42
相关思维导图模板

树图思维导图提供 经典一年级数学3和4的组成和分解教案5篇 在线思维导图免费制作,点击“编辑”按钮,可对 经典一年级数学3和4的组成和分解教案5篇 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:41b5245d18ebce611ff0c162e9f10474

树图思维导图提供 苏教一年级数学下册教案2021 在线思维导图免费制作,点击“编辑”按钮,可对 苏教一年级数学下册教案2021 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6c038f2cb24cafe3208f9f1fdb9eb1a9









 上海工商
上海工商