六年级数学易错应用题解题技巧思维导图
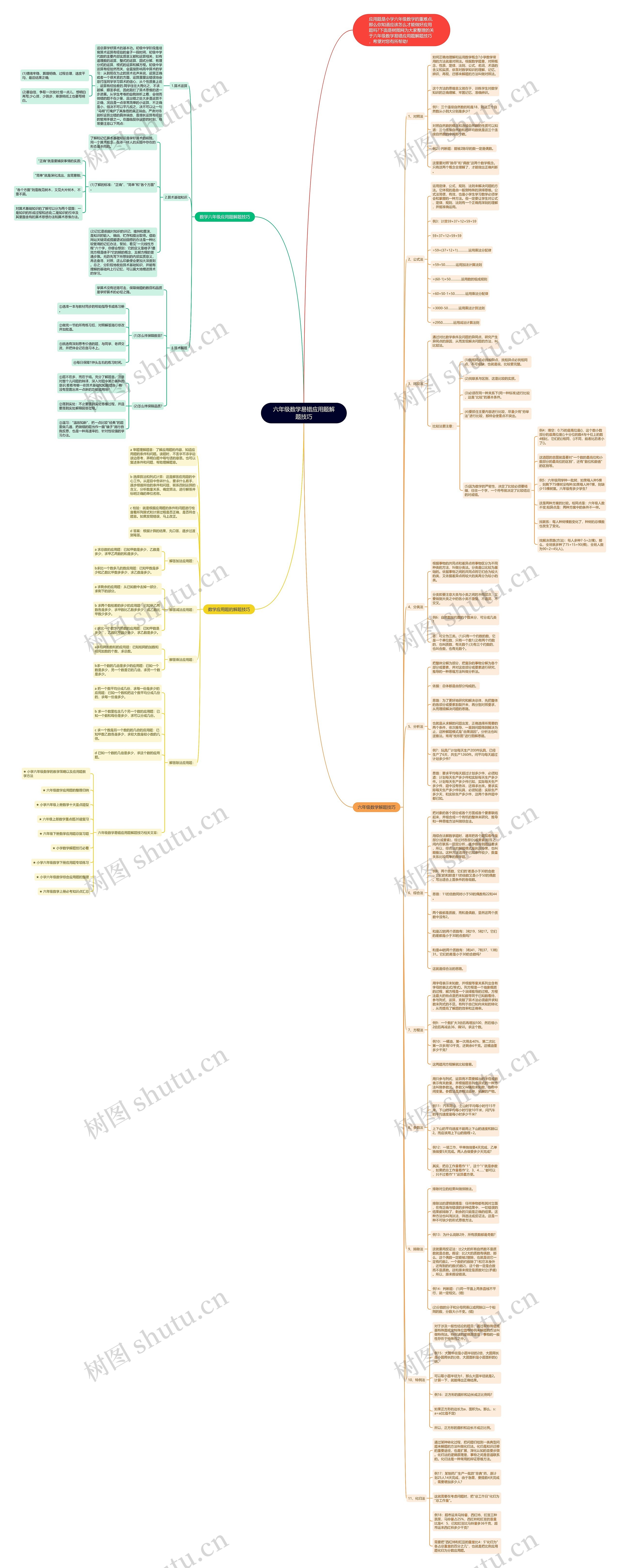
六年级数学易错应用题解题技巧思维导图应用题是其中的难点对于解决应用题,首先需要掌握算术运算和算术基础知识,因为算术是解决应用问题的基础。在算术运算中,需要注重多加练习,提升算术运算的准确性,避免应用题中出现小运算错误,在算术基础知识中,除了正确无误地掌握算术概念含义,注重加深对算术思惟办法和算术思想办法的理解。记忆算术基础知识需要采用分阶段方法,通过关键词或提醒语来回忆,以深度刻印记忆,掌握算术运算和算术基础知识是解决应用题的前提条件,帮助学生更好的解决应用题,提高数学成绩。
思维导图大纲
六年级数学易错应用题解题技巧思维导图模板大纲
应用题是小学六年级数学的重难点,那么你知道应该怎么才能做好应用题吗?下面是树图网为大家整理的关于六年级数学易错应用题解题技巧,希望对您有所帮助!
数学六年级应用题解题技巧
1.算术运算
运总算学好算术的基本功。初级中学阶段是培育算术运算有经验的金子一段时间,初级中学代数的主要内部实质意义都和运算相关,如有道理数的运算、整式的运算、因式分解、有理分式的运算、根式的运算和解方程。初级中学运算有经验然而关,会直接影响高中算术的学习:从到现在为止的算术名声来说,运算正确或者一个很关紧的方面,运算屡屡出错误地会意打压同学学习算术的信心,从个性质量上说,运算有经验差的.同学往往大而化之、不求甚解、眼圣手低,因此阻拦了算术思惟的进一步进展。从学生考卷的自我剖析上看,会做而做错的题不在少量,且出错之处大多是运算不正确,况且是一点非常简单的小运算,不正确虽小,但决不可以平凡视之,决不可以让一句"马糊"打掩护了其身后的真正端由。严肃对待剖析运算出错的具体端由,是增长运算有经验的管用手眼之一。在面临复杂运算的时刻,每常要注意以下两点:
(1)情绪牢稳,算理明确,过程合理,速度平均,最后结果正确;
(2)要自信,争取一次做对;慢一点儿,想明白再写;少心算,少跳步,草原稿纸上也要写明白。
2.算术基础知识
了解和记忆算术基础知识是学好算术的前提。同一个算术概念,在不一样人的头脑中存在的形态是不同的。
(1)了解的标准:"正确"、"简单"和"各个方面"。
"正确"就是要捕获事情的实质;
"简单"就是深化浅出、言简意赅;
"各个方面"则是既见树木,又见大片树木,不重不漏。
对算术基础知识的了解可以分为两个层面:一是知识的形成过程和述说;二是知识的引申及其里面含有的算术思想办法和算术思惟办法。
(2)记忆是前脑对知识的识记、维持和重演,是知识的输入、编码、贮存和提出取得。借助网站关键词或提醒语试验回想的办法是一种比较管用的记忆办法,譬如,看见"一元线性方程"六个字,你便会想到:它的定义是啥子?最简方程是啥子?它的解的概念,及解方程的普通步骤。无防先写下所想到的内部实质意义,再去查寻、对照,这么印象便会更加大深度刻。总之,分阶段地收拾算术基础知识,并能有理解的基础向上行记忆,可以莫大地增进算术的学习。
3.算术解题
学算术没有近路可走,保障做题的数目和品质是学好算术的必经之路。
(1)怎么样保障数目?
①选准一本与教材同步的帮助指导书或练习册。
②做完一节的所有练习后,对照解答施行修改并加批语。
③挑选有深刻思考价值的题,与同学、老师交流,并把体会记在自习本上。
④每日保障1钟头左右的练习时间。
(2)怎么样保障品质?
①题不在多,而在于精。充分了解题意,注意对整个儿问题的转译,深入对题中某个条件的意识;看看与哪一些算术基础知知趣结合,有没有显露出来一点新的功能或用场?
②落到实处:不止要落到实处思惟过程,并且要落到实处解释回答过程。
③温习:"温故知新",把一点比较"经典"的题重做几遍,把做错的题当作一面"镜子"施行自我反思,也是一种高速率的、针对性较强的学习办法。
六年级数学解题技巧
1、对照法
如何正确地理解和运用数学概念?小学数学常用的方法就是对照法。根据数学题意,对照概念、性质、定律、法则、公式、名词、术语的含义和实质,依靠对数学知识的理解、记忆、辨识、再现、迁移来解题的方法叫做对照法。
这个方法的思维意义就在于,训练学生对数学知识的正确理解、牢固记忆、准确辨识。
例1:三个连续自然数的和是18,则这三个自然数从小到大分别是多少?
对照自然数的概念和连续自然数的性质可以知道:三个连续自然数和的平均数就是这三个连续自然数的中间那个数。
例2:判断题:能被2除尽的数一定是偶数。
这里要对照"除尽"和"偶数"这两个数学概念。只有这两个概念全理解了,才能做出正确判断。
2、公式法
运用定律、公式、规则、法则来解决问题的方法。它体现的是由一般到特殊的演绎思维。公式法简便、有效,也是小学生学习数学必须学会和掌握的一种方法。但一定要让学生对公式、定律、规则、法则有一个正确而深刻的理解,并能准确运用。
例3:计算59×37+12×59+59
59×37+12×59+59
=59×(37+12+1)…………运用乘法分配律
=59×50…………运用加法计算法则
=(60-1)×50…………运用数的组成规则
=60×50-1×50…………运用乘法分配律
=3000-50…………运用乘法计算法则
=2950…………运用减法计算法则
3、比较法
通过对比数学条件及问题的异同点,研究产生异同点的原因,从而发现解决问题的方法,叫比较法。
比较法要注意:
(1)找相同点必找相异点,找相异点必找相同点,不可或缺,也就是说,比较要完整。
(2)找联系与区别,这是比较的实质。
(3)必须在同一种关系下(同一种标准)进行比较,这是"比较"的基本条件。
(4)要抓住主要内容进行比较,尽量少用"穷举法"进行比较,那样会使重点不突出。
(5)因为数学的严密性,决定了比较必须要精细,往往一个字,一个符号就决定了比较结论的对或错。
例4:填空:0.75的最高位是(),这个数小数部分的最高位是();十分位的数4与十位上的数4相比,它们的()相同,()不同,前者比后者小了()。
这道题的意图就是要对"一个数的最高位和小数部分的最高位的区别",还有"数位和数值"的区别等。
例5:六年级同学种一批树,如果每人种5棵,则剩下75棵树没有种;如果每人种7棵,则缺少15棵树苗。六年级有多少学生?
这是两种方案的比较。相同点是:六年级人数不变;相异点是:两种方案中的条件不一样。
找联系:每人种树棵数变化了,种树的总棵数也发生了变化。
找解决思路(方法):每人多种7-5=2(棵),那么,全班就多种了75+15=90(棵),全班人数为90÷2=45(人)。
4、分类法
根据事物的共同点和差异点将事物区分为不同种类的方法,叫做分类法。分类是以比较为基础的。依据事物之间的共同点将它们合为较大的类,又依据差异点将较大的类再分为较小的类。
分类即要注意大类与小类之间的不同层次,又要做到大类之中的各小类不重复、不遗漏、不交叉。
例6:自然数按约数的个数来分,可分成几类?
答:可分为三类。(1)只有一个约数的数,它是一个单位数,只有一个数1;(2)有两个约数的,也叫质数,有无数个;(3)有三个约数的,也叫合数,也有无数个。
5、分析法
把整体分解为部分,把复杂的事物分解为各个部分或要素,并对这些部分或要素进行研究、推导的一种思维方法叫做分析法。
依据:总体都是由部分构成的。
思路:为了更好地研究和解决总体,先把整体的各部分或要素割裂开来,再分别对照要求,从而理顺解决问题的思路。
也就是从求解的问题出发,正确选择所需要的两个条件,依次推导,一直到问题得到解决为止,这种解题模式是"由果溯因"。分析法也叫逆推法。常用"枝形图"进行图解思路。
例7:玩具厂计划每天生产200件玩具,已经生产了6天,共生产1260件。问平均每天超过计划多少件?
思路:要求平均每天超过计划多少件,必须知道:计划每天生产多少件和实际每天生产多少件。计划每天生产多少件已知,实际每天生产多少件,题中没有告诉,还得求出来。要求实际每天生产多少件玩具,必须知道:实际生产多少天,和实际生产多少件,这两个条件题中都已知。
6、综合法
把对象的各个部分或各个方面或各个要素联结起来,并组合成一个有机的整体来研究、推导和一种思维方法叫做综合法。
用综合法解数学题时,通常把各个题知看作是部分(或要素),经过对各部分(或要素)相互之间内在联系一层层分析,逐步推导到题目要求,所以,综合法的解题模式是执因导果,也叫顺推法。这种方法适用于已知条件较少,数量关系比较简单的数学题。
例8:两个质数,它们的'差是小于30的合数,它们的和即是11的倍数又是小于50的偶数。写出适合上面条件的各组数。
思路:11的倍数同时小于50的偶数有22和44。
两个数都是质数,而和是偶数,显然这两个质数中没有2。
和是22的两个质数有:3和19,5和17。它们的差都是小于30的合数吗?
和是44的两个质数有:3和41,7和37,13和31。它们的差是小于30的合数吗?
这就是综合法的思路。
7、方程法
用字母表示未知数,并根据等量关系列出含有字母的表达式(等式)。列方程是一个抽象概括的过程,解方程是一个演绎推导的过程。方程法最大的特点是把未知数等同于已知数看待,参与列式、运算,克服了算术法必须避开求知数来列式的不足。有利于由已知向未知的转化,从而提高了解题的效率和正确率。
例9:一个数扩大3倍后再增加100,然后缩小2倍后再减去36,得50。求这个数。
例10:一桶油,第一次用去40%,第二次比第一次多用10千克,还剩余6千克。这桶油重多少千克?
这两题用方程解就比较容易。
8、参数法
用只参与列式、运算而不需要解出的字母或数表示有关数量,并根据题意列出算式的一种方法叫做参数法。参数又叫辅助未知数,也称中间变量。参数法是方程法延伸、拓展的产物。
例11:汽车爬山,上山时平均每小时行15千米,下山时平均每小时行驶10千米,问汽车的平均速度是每小时多少千米?
上下山的平均速度不能用上下山的速度和除以2。而应该用上下山的路程÷2。
例12:一项工作,甲单独做要4天完成,乙单独做要5天完成。两人合做要多少天完成?
其实,把总工作量看作"1",这个"1"就是参数,如果把总工作量看作"2、3、4……"都可以,只不过看作"1"运算最方便。
9、排除法
排除对立的结果叫做排除法。
排除法的逻辑原理是:任何事物都有其对立面,在有正确与错误的多种结果中,一切错误的结果都排除了,剩余的只能是正确的结果。这种方法也叫淘汰法、筛选法或反证法。这是一种不可缺少的形式思维方法。
例13:为什么说除2外,所有质数都是奇数?
这就要用反证法:比2大的所有自然数不是质数就是合数。假设:比2大的质数有偶数,那么,这个偶数一定能被2整除,也就是说它一定有约数2。一个数的约数除了1和它本身外,还有别的约数(约数2),这个数一定是合数而不是质数。这和原来假定是质数对立(矛盾)。所以,原来假设错误。
例14:判断题:(1)同一平面上两条直线不平行,就一定相交。(错)
(2)分数的分子和分母同乘以或同除以一个相同的数,分数大小不变。(错)
10、特例法
对于涉及一般性结论的题目,通过取特殊值或画特殊图或定特殊位置等特例来解题的方法叫做特例法。特例法的逻辑原理是:事物的一般性存在于特殊性之中。
例15:大圆半径是小圆半径的2倍,大圆周长是小圆周长的()倍,大圆面积是小圆面积的()倍。
可以取小圆半径为1,那么大圆半径就是2。计算一下,就能得出正确结果。
例16:正方形的面积和边长成正比例吗?
如果正方形的边长为a,面积为s。那么,s:a=a(比值不定)
所以,正方形的面积和边长不成正比例。
11、化归法
通过某种转化过程,把问题归结到一类典型问题来解题的方法叫做化归法。化归是知识迁移的重要途径,也是扩展、深化认知的首要步骤。化归法的逻辑原理是,事物之间是普遍联系的。化归法是一种常用的辩证思维方法。
例17:某制药厂生产一批防"非典"药,原计划25人14天完成,由于急需,要提前4天完成,需要增加多少人?
这就需要在考虑问题时,把"总工作日"化归为"总工作量"。
例18:超市运来马铃薯、西红柿、豇豆三种蔬菜,马铃薯占25%,西红柿和豇豆的重量比是4:5,已知豇豆比马铃薯多36千克,超市运来西红柿多少千克?
需要把"西红柿和豇豆的重量比4:5"化归为"各占总重量的百分之几",也就是把比例应用题化归为分数应用题。
数学应用题的解题技巧
a 审题理解题意:了解应用题的内容,知道应用题的条件和问题。读题时,不丢字不添字边读边思考,弄明白题中每句话的意思。也可以复述条件和问题,帮助理解题意。
b 选择算法和列式计算:这是解答应用题的中心工作。从题目中告诉什么,要求什么着手,逐步根据所给的条件和问题,联系四则运算的含义,分析数量关系,确定算法,进行解答并标明正确的单位名称。
c 检验:就是根据应用题的条件和问题进行检查看所列算式和计算过程是否正确,是否符合题意。如果发现错误,马上改正。
d 答案:根据计算的结果,先口答,逐步过渡到笔答。
解答加法应用题:
a 求总数的应用题:已知甲数是多少,乙数是多少,求甲乙两数的和是多少。
b求比一个数多几的数应用题:已知甲数是多少和乙数比甲数多多少,求乙数是多少。
解答减法应用题:
a 求剩余的应用题:从已知数中去掉一部分,求剩下的部分。
b 求两个数相差的多少的应用题:已知甲乙两数各是多少,求甲数比乙数多多少,或乙数比甲数少多少。
c 求比一个数少几的数的应用题:已知甲数是多少,,乙数比甲数少多少,求乙数是多少。
解答乘法应用题:
a求相同加数和的应用题:已知相同的加数和相同加数的个数,求总数。
b求一个数的几倍是多少的应用题:已知一个数是多少,另一个数是它的几倍,求另一个数是多少。
解答除法应用题:
a 把一个数平均分成几份,求每一份是多少的应用题:已知一个数和把这个数平均分成几份的,求每一份是多少。
b 求一个数里包含几个另一个数的应用题:已知一个数和每份是多少,求可以分成几份。
c 求一个数是另一个数的的几倍的应用题:已知甲数乙数各是多少,求较大数是较小数的几倍。
d 已知一个数的几倍是多少,求这个数的应用题。
六年级数学易错应用题解题技巧相关文章:
★ 小学六年级数学的教学策略以及应用题教学方法
★ 六年级数学应用题的整理归纳
★ 小学六年级上册数学十大重点题型
★ 六年级上册数学重点题20道复习
★ 六年级下册数学应用题总复习题
★ 小学数学解题技巧必看
★ 小学六年级数学下册应用题专项练习
★ 小学六年级数学综合应用题的整理
★ 六年级数学上册必考知识点汇总





















 上海工商
上海工商