数学中考知识点总结思维导图

数学中考知识点总结思维导图互余角的三角函数间的关系、二次函数的解析式和如何决定抛物线的特征,如对称轴的位置、顶点坐标、开口方向等。掌握这些知识点可以帮助考生更好的备考数学中考,更快更准确地解决相关数学问题,了解函数图象的平移方式,可以更加灵活地运用解题技巧,建议多温故知新,总结经验,扎实提高数学解题能力。
思维导图大纲
数学中考知识点总结思维导图模板大纲
每一门科目都有自己的学习方法,但其实都是万变不离其中的,数学其实和语文英语一样,也是要记、要背、要讲练的。下面是树图网给大家整理的一些关于数学中考的知识点,希望对大家有所帮助。
中考数学知识点汇总
锐角三角函数定义
锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
正弦(sin)等于对边比斜边;sinA=a/c
余弦(cos)等于邻边比斜边;cosA=b/c
正切(tan)等于对边比邻边;tanA=a/b
余切(cot)等于邻边比对边;cotA=b/a
正割(sec)等于斜边比邻边;secA=c/b
余割(csc)等于斜边比对边。cscA=c/a
互余角的三角函数间的关系
sin(90°-α)=cosα,cos(90°-α)=sinα,
tan(90°-α)=cotα,cot(90°-α)=tanα.
平方关系:
sin^2(α)+cos^2(α)=1
tan^2(α)+1=sec^2(α)
cot^2(α)+1=csc^2(α)
积的关系:
sinα=tanα·cosα
cosα=cotα·sinα
tanα=sinα·secα
cotα=cosα·cscα
secα=tanα·cscα
cscα=secα·cotα
倒数关系:
tanα·cotα=1
sinα·cscα=1
cosα·secα=1
中考数学知识点
二次函数的解析式有三种形式:
(1)一般式:
(2)顶点式:
(3)当抛物线与x轴有交点时,即对应二次好方程有实根和存在时,根据二次三项式的分解因式,二次函数可转化为两根式。如果没有交点,则不能这样表示。
注意:抛物线位置由决定.
(1)决定抛物线的开口方向
①开口向上.
②开口向下.
(2)决定抛物线与y轴交点的位置.
①图象与y轴交点在x轴上方.
②图象过原点.
③图象与y轴交点在x轴下方.
(3)决定抛物线对称轴的位置(对称轴:)
①同号对称轴在y轴左侧.
②对称轴是y轴.
③异号对称轴在y轴右侧.
(4)顶点坐标.
(5)决定抛物线与x轴的交点情况.、
①△>0抛物线与x轴有两个不同交点.
②△=0抛物线与x轴有的公共点(相切).
③△<0抛物线与x轴无公共点.
(6)二次函数是否具有、最小值由a判断.
①当a>0时,抛物线有最低点,函数有最小值.
②当a<0时,抛物线有点,函数有值.
(7)的符号的判定:
表达式,请代值,对应y值定正负;
对称轴,用处多,三种式子相约;
轴两侧判,左同右异中为0;
1的两侧判,左同右异中为0;
-1两侧判,左异右同中为0.
(8)函数图象的平移:左右平移变x,左+右-;上下平移变常数项,上+下-;平移结果先知道,反向平移是诀窍;平移方式不知道,通过顶点来寻找。
(9)对称:关于x轴对称的解析式为,关于y轴对称的解析式为,关于原点轴对称的解析式为,在顶点处翻折后的解析式为(a相反,定点坐标不变)。
(10)结论:①二次函数(与x轴只有一个交点二次函数的顶点在x轴上Δ=0;
②二次函数(的顶点在y轴上二次函数的图象关于y轴对称;
③二次函数(经过原点,则。
(11)二次函数的解析式:
①一般式:(,用于已知三点。
②顶点式:,用于已知顶点坐标或最值或对称轴。
(3)交点式:,其中、是二次函数与x轴的两个交点的横坐标。若已知对称轴和在x轴上的截距,也可用此式。
中考数学知识点:直角三角形
一、三角函数
1.定义:在Rt△ABC中,∠C=Rt∠,则sinA= ;cosA= ;tgA= ;ctgA= .
2. 特殊角的三角函数值:
0° 30° 45° 60° 90°
sinα
cosα
tgα /
ctgα /
3. 互余两角的三角函数关系:sin(90°-α)=cosα;…
4. 三角函数值随角度变化的关系
5.查三角函数表
二、解直角三角形
1. 定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
2. 依据:①边的关系:
②角的关系:A+B=90°
③边角关系:三角函数的定义。
注意:尽量避免使用中间数据和除法。
三、对实际问题的处理
1. 俯、仰角: 2.方位角、象限角: 3.坡度:
4.在两个直角三角形中,都缺解直角三角形的条件时,可用列方程的办法解决。
数学中考知识点总结相关文章:
★ 数学中考考点
★ 2021中考数学知识点归纳(最新完整版)
★ 2021中考数学必考知识点归纳
★ 2021中考数学重点知识点归纳
★ 中考数学知识点归纳总结2021
★ 初中数学考点归纳整理
★ 初中数学中考考点归纳总结2021
★ 数学必考知识点初中整理
★ 2021中考数学重点知识点梳理归纳
★ 初三数学重点难点考点归纳
相关思维导图模板

树图思维导图提供 苏教数学中考知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 苏教数学中考知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:84dedad001f9c49341c3f42c27c3e0b7

树图思维导图提供 中考知识点总结数学 在线思维导图免费制作,点击“编辑”按钮,可对 中考知识点总结数学 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7eb5b337158011c81c2804a6702df847












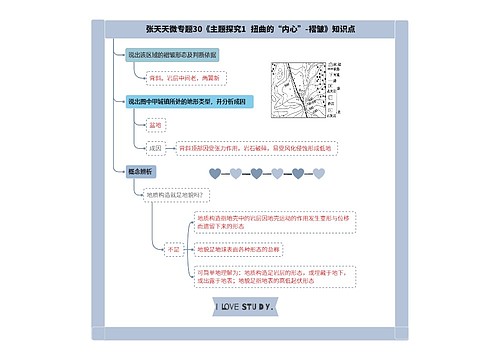
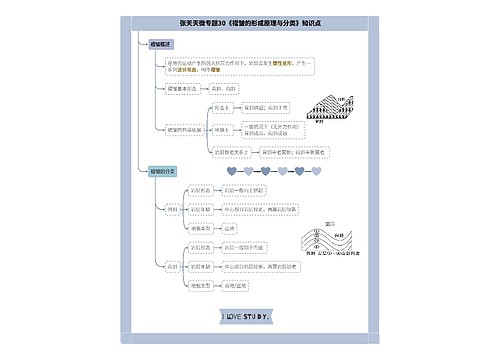



 上海工商
上海工商