二次函数知识点|2022年九年级数学思维导图
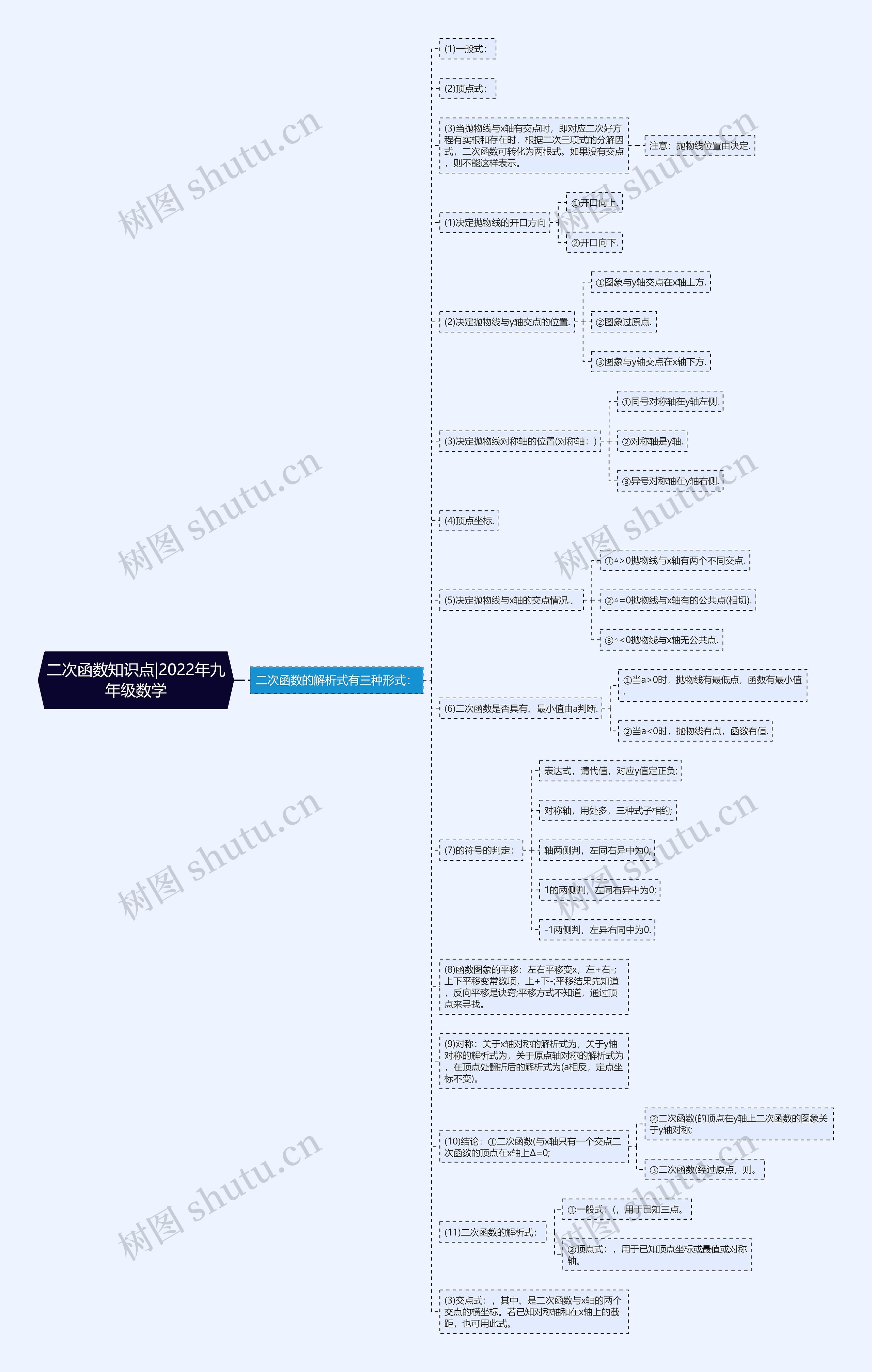
二次函数知识点|2022年九年级数学思维导图,二次函数的解析式有三种形式:一般式、顶点式和交点式,决定抛物线位置的因素有抛物线开口方向、与y轴交点的位置、对称轴的位置、顶点坐标和与x轴的交点情况。二次函数是否具有最小值由a判断。符号的判定方式为对表达式代值,并对应y值定正负,对称轴可用三种式子相约进行计算,左同右异中为0,左异右同中为-1,函数图象的平移方式为左+右-变x,上+下-变常数项。关于对称,解析式可分为关于x轴对称、关于y轴对称和关于原点对称的,在顶点处翻折后的解析式为(a相反,定点坐标不变),掌握一般式、顶点式和交点式作为二次函数的解析式,可以应用于已知三点、已知顶点坐标或最值或对称轴和已知对称轴和在x轴上的截距。
思维导图大纲
二次函数知识点|2022年九年级数学思维导图模板大纲
二次函数的解析式有三种形式:
(1)一般式:
(2)顶点式:
(3)当抛物线与x轴有交点时,即对应二次好方程有实根和存在时,根据二次三项式的分解因式,二次函数可转化为两根式。如果没有交点,则不能这样表示。
注意:抛物线位置由决定.
(1)决定抛物线的开口方向
①开口向上.
②开口向下.
(2)决定抛物线与y轴交点的位置.
①图象与y轴交点在x轴上方.
②图象过原点.
③图象与y轴交点在x轴下方.
(3)决定抛物线对称轴的位置(对称轴:)
①同号对称轴在y轴左侧.
②对称轴是y轴.
③异号对称轴在y轴右侧.
(4)顶点坐标.
(5)决定抛物线与x轴的交点情况.、
①△>0抛物线与x轴有两个不同交点.
②△=0抛物线与x轴有的公共点(相切).
③△<0抛物线与x轴无公共点.
(6)二次函数是否具有、最小值由a判断.
①当a>0时,抛物线有最低点,函数有最小值.
②当a<0时,抛物线有点,函数有值.
(7)的符号的判定:
表达式,请代值,对应y值定正负;
对称轴,用处多,三种式子相约;
轴两侧判,左同右异中为0;
1的两侧判,左同右异中为0;
-1两侧判,左异右同中为0.
(8)函数图象的平移:左右平移变x,左+右-;上下平移变常数项,上+下-;平移结果先知道,反向平移是诀窍;平移方式不知道,通过顶点来寻找。
(9)对称:关于x轴对称的解析式为,关于y轴对称的解析式为,关于原点轴对称的解析式为,在顶点处翻折后的解析式为(a相反,定点坐标不变)。
(10)结论:①二次函数(与x轴只有一个交点二次函数的顶点在x轴上Δ=0;
②二次函数(的顶点在y轴上二次函数的图象关于y轴对称;
③二次函数(经过原点,则。
(11)二次函数的解析式:
①一般式:(,用于已知三点。
②顶点式:,用于已知顶点坐标或最值或对称轴。
(3)交点式:,其中、是二次函数与x轴的两个交点的横坐标。若已知对称轴和在x轴上的截距,也可用此式。
相关思维导图模板

树图思维导图提供 沪教版九年级上册数学知识点【四篇】 在线思维导图免费制作,点击“编辑”按钮,可对 沪教版九年级上册数学知识点【四篇】 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:42f86837ece905cd3decd3f994533cb6


树图思维导图提供 2022年九年级数学数学反思 在线思维导图免费制作,点击“编辑”按钮,可对 2022年九年级数学数学反思 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:294b84516182055ef84e52b875c6bdc7


















 上海工商
上海工商