中学数学知识点:平行线的性质和判定思维导图
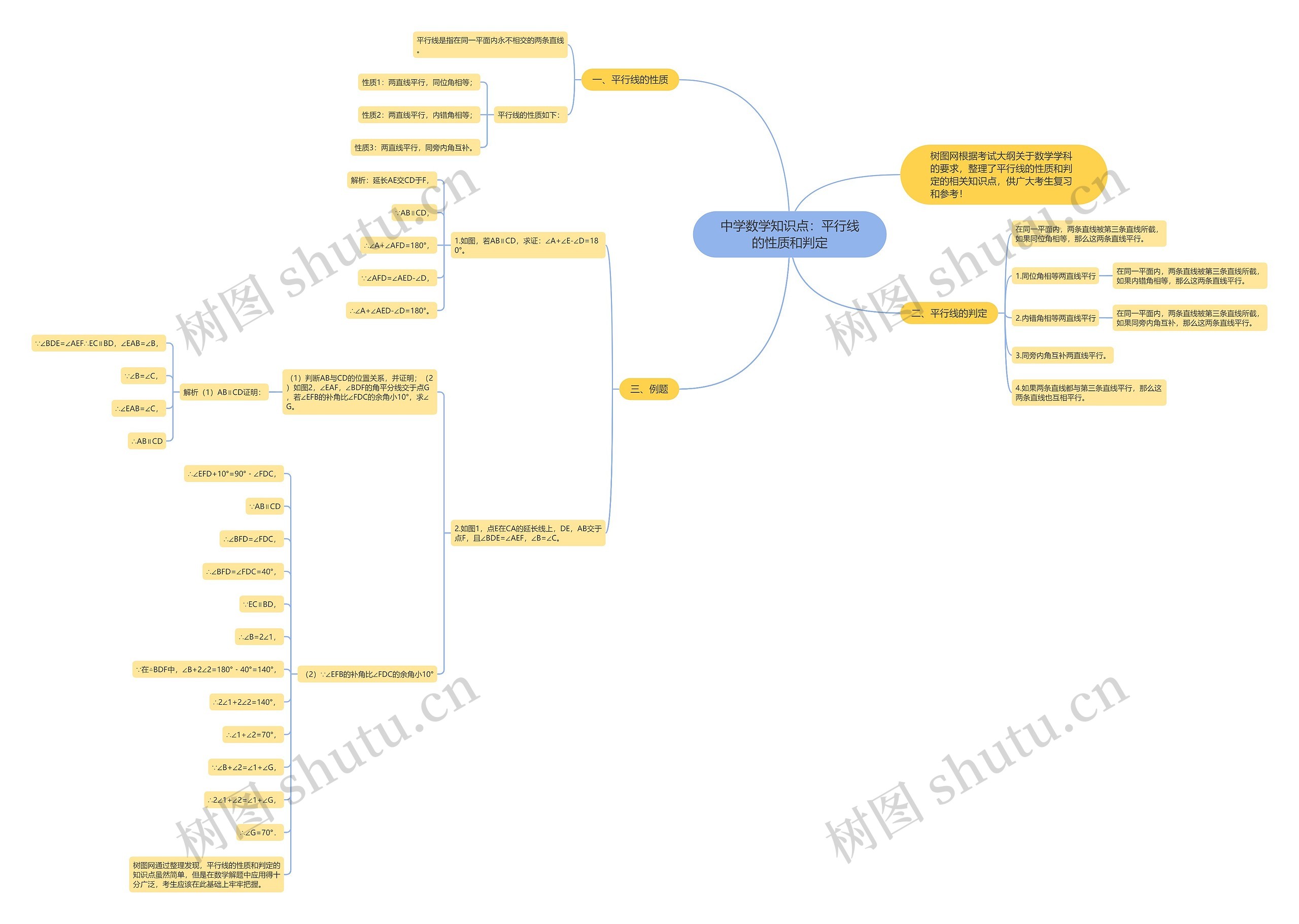
中学数学知识点:平行线的性质和判定思维导图包含平行线的性质和判定,两条直线平行时,同位角相等、内错角相等、同旁内角互补,在同一平面内,如果两条直线第三条直线所截,同位角相等则这两条直线平行,如果内错角相等则这两条直线平行,如果同旁内角互补则这两条直线平行,例题包含了证明和计算题,需要掌握平行线的性质和判定思路,多练习平行线的计算和证明题目。
思维导图大纲
中学数学知识点:平行线的性质和判定思维导图模板大纲
树图网根据考试大纲关于数学学科的要求,整理了平行线的性质和判定的相关知识点,供广大考生复习和参考!
一、平行线的性质
平行线是指在同一平面内永不相交的两条直线。
平行线的性质如下:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补。
二、平行线的判定
在同一平面内,两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
1.同位角相等两直线平行
在同一平面内,两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
2.内错角相等两直线平行
在同一平面内,两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
3.同旁内角互补两直线平行。
4.如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
三、例题
1.如图,若AB∥CD,求证:∠A+∠E-∠D=180°。
解析:延长AE交CD于F,
∵AB∥CD,
∴∠A+∠AFD=180°,
∵∠AFD=∠AED-∠D,
∴∠A+∠AED-∠D=180°。
2.如图1,点E在CA的延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C。
(1)判断AB与CD的位置关系,并证明;(2)如图2,∠EAF,∠BDF的角平分线交于点G,若∠EFB的补角比∠FDC的余角小10°,求∠G。
解析(1)AB∥CD证明:
∵∠BDE=∠AEF∴EC∥BD,∠EAB=∠B,
∵∠B=∠C,
∴∠EAB=∠C,
∴AB∥CD
(2)∵∠EFB的补角比∠FDC的余角小10°
∴∠EFD+10°=90°﹣∠FDC,
∵AB∥CD
∴∠BFD=∠FDC,
∴∠BFD=∠FDC=40°,
∵EC∥BD,
∴∠B=2∠1,
∵在△BDF中,∠B+2∠2=180°﹣40°=140°,
∴2∠1+2∠2=140°,
∴∠1+∠2=70°,
∵∠B+∠2=∠1+∠G,
∴2∠1+∠2=∠1+∠G,
∴∠G=70°.
树图网通过整理发现,平行线的性质和判定的知识点虽然简单,但是在数学解题中应用得十分广泛,考生应该在此基础上牢牢把握。
相关思维导图模板

树图思维导图提供 中考数学难点知识复习资料 在线思维导图免费制作,点击“编辑”按钮,可对 中考数学难点知识复习资料 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:29bb4378dea38ac36ae1bf6c9973a557

树图思维导图提供 初中数学分式知识点 在线思维导图免费制作,点击“编辑”按钮,可对 初中数学分式知识点 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6eaf7c2b61ff0c7b59c31db58324e842







 上海工商
上海工商