高一数学教案:函数的基本概念思维导图
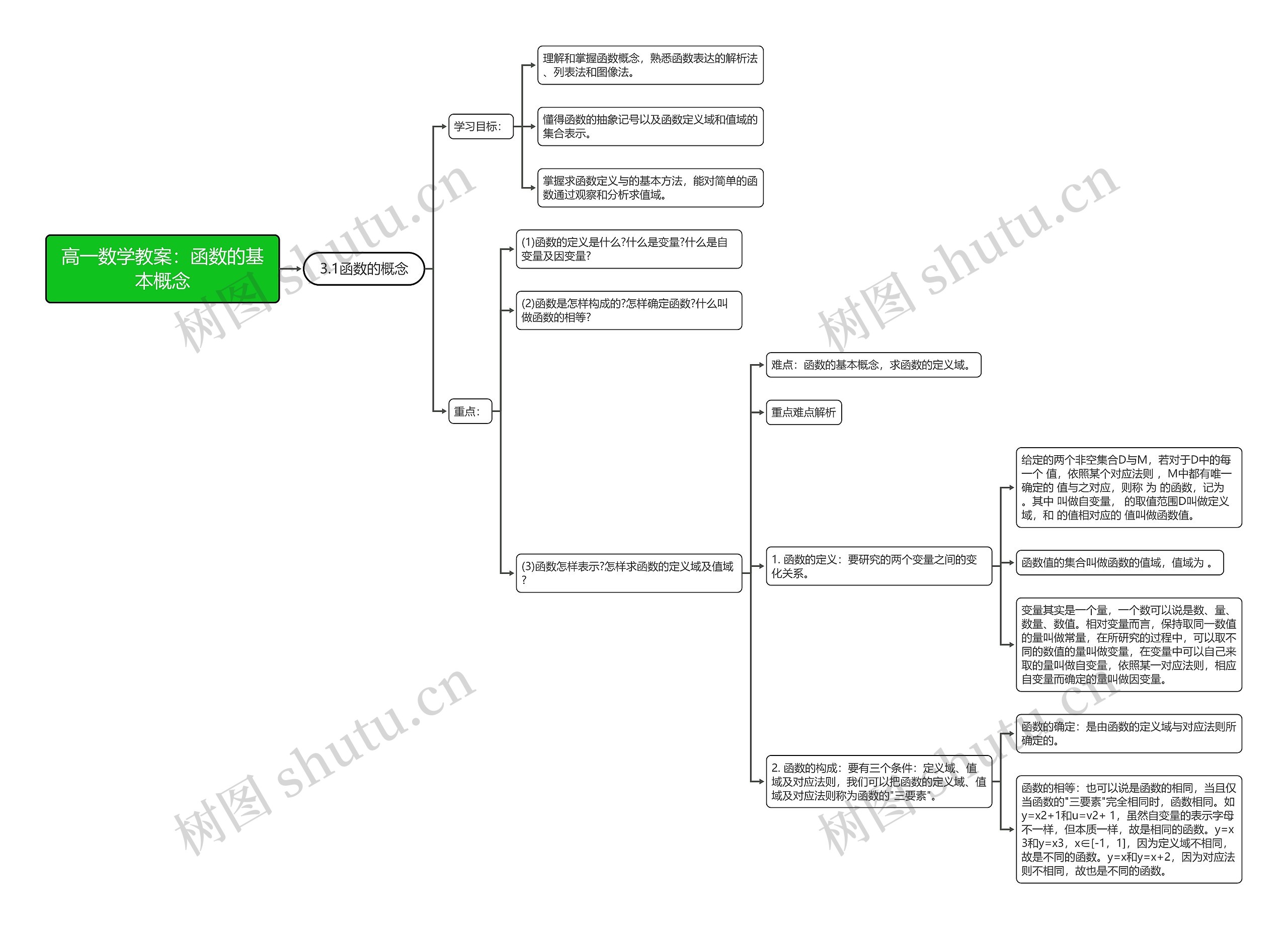
本教案讲解了高一数学中关于函数的基本概念和思维导图模板大纲,的知识点有函数的定义,变量的概念和自变量和因变量的含义,函数的构成要素包含定义域、值域和对应法则,函数的确定是由定义域和对应法则所确定的,函数的相等是指三要素完全相同的函数,函数的定义域及求解是重点难点。
思维导图大纲
高一数学教案:函数的基本概念思维导图模板大纲
3.1函数的概念
学习目标:
理解和掌握函数概念,熟悉函数表达的解析法、列表法和图像法。
懂得函数的抽象记号以及函数定义域和值域的集合表示。
掌握求函数定义与的基本方法,能对简单的函数通过观察和分析求值域。
重点:
(1)函数的定义是什么?什么是变量?什么是自变量及因变量?
(2)函数是怎样构成的?怎样确定函数?什么叫做函数的相等?
(3)函数怎样表示?怎样求函数的定义域及值域?
难点:函数的基本概念,求函数的定义域。
重点难点解析
1. 函数的定义:要研究的两个变量之间的变化关系。
给定的两个非空集合D与M,若对于D中的每一个 值,依照某个对应法则 ,M中都有唯一确定的 值与之对应,则称 为 的函数,记为 。其中 叫做自变量, 的取值范围D叫做定义域,和 的值相对应的 值叫做函数值。
函数值的集合叫做函数的值域,值域为 。
变量其实是一个量,一个数可以说是数、量、数量、数值。相对变量而言,保持取同一数值的量叫做常量,在所研究的过程中,可以取不同的数值的量叫做变量,在变量中可以自己来取的量叫做自变量,依照某一对应法则,相应自变量而确定的量叫做因变量。
2. 函数的构成:要有三个条件:定义域、值域及对应法则,我们可以把函数的定义域、值域及对应法则称为函数的"三要素"。
函数的确定:是由函数的定义域与对应法则所确定的。
函数的相等:也可以说是函数的相同,当且仅当函数的"三要素"完全相同时,函数相同。如y=x2+1和u=v2+ 1,虽然自变量的表示字母不一样,但本质一样,故是相同的函数。y=x3和y=x3,x∈[-1,1],因为定义域不相同,故是不同的函数。y=x和y=x+2,因为对应法则不相同,故也是不同的函数。
相关思维导图模板


树图思维导图提供 高一数学教案计划大全 在线思维导图免费制作,点击“编辑”按钮,可对 高一数学教案计划大全 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0a41e1e93d3d4a9f88aebc05d0a1a53d








 上海工商
上海工商