高二数学教案:组合(3)思维导图
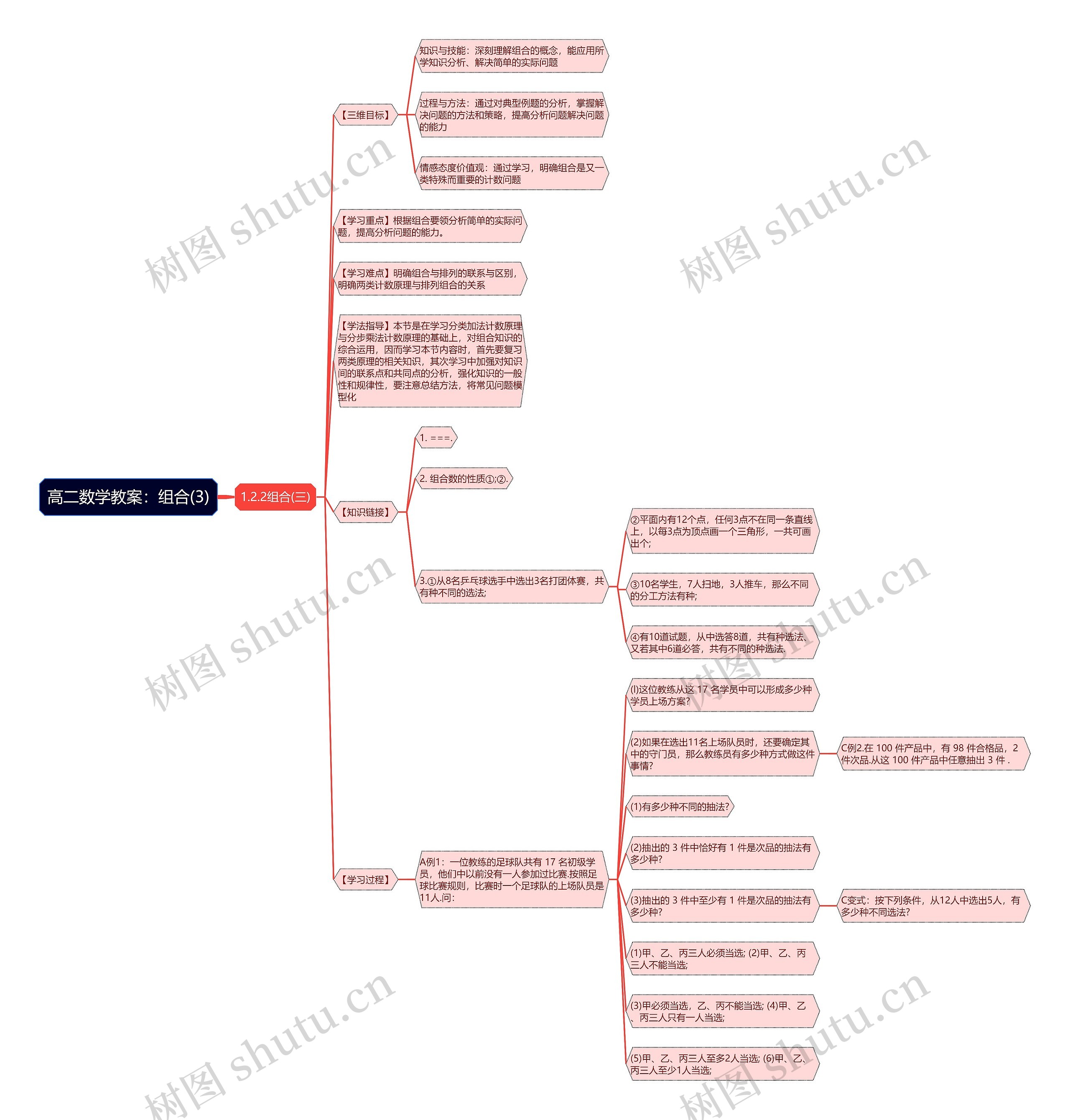
这是一个高二数学教案,主题是组合(3)思维导图,在这次中,学生将深入理解组合的概念,并能够应用所学知识来分析和解决简单的实际问题,通过对典型例题的分析,学生将掌握解决问题的方法和策略,问题分析和解决能力。通过学习,学生将明确组合是一类特殊而重要的计数问题,学习重点是根据组合要领分析简单的实际问题,提高问题分析的能力,学习难点是明确组合与排列的联系与区别,和两类计数原理与排列组合的关系。在学习这次的内容时,要复习两类原理的相关知识,其次要加强对知识间的联系和共同点的分析,强化知识的一般性和规律性,并注意总结方法,将常见问题模型化。知识链接包含组合数的性质,和一些具体的问题模型,在学习过程中,还会进行一些例题讲解,例如关于足球队的上场方案的问题和从产品中抽取的问题,还会给出一些变式问题供学生练习。
思维导图大纲
高二数学教案:组合(3)思维导图模板大纲
1.2.2组合(三)
【三维目标】
知识与技能:深刻理解组合的概念,能应用所学知识分析、解决简单的实际问题
过程与方法:通过对典型例题的分析,掌握解决问题的方法和策略,提高分析问题解决问题的能力
情感态度价值观:通过学习,明确组合是又一类特殊而重要的计数问题
【学习重点】根据组合要领分析简单的实际问题,提高分析问题的能力。
【学习难点】明确组合与排列的联系与区别,明确两类计数原理与排列组合的关系
【学法指导】本节是在学习分类加法计数原理与分步乘法计数原理的基础上,对组合知识的综合运用,因而学习本节内容时,首先要复习两类原理的相关知识,其次学习中加强对知识间的联系点和共同点的分析,强化知识的一般性和规律性,要注意总结方法,将常见问题模型化
【知识链接】
1. ===.
2. 组合数的性质①;②.
3.①从8名乒乓球选手中选出3名打团体赛,共有种不同的选法;
②平面内有12个点,任何3点不在同一条直线上,以每3点为顶点画一个三角形,一共可画出个;
③10名学生,7人扫地,3人推车,那么不同的分工方法有种;
④有10道试题,从中选答8道,共有种选法、又若其中6道必答,共有不同的种选法.
【学习过程】
A例1:一位教练的足球队共有 17 名初级学员,他们中以前没有一人参加过比赛.按照足球比赛规则,比赛时一个足球队的上场队员是11人.问:
(l)这位教练从这 17 名学员中可以形成多少种学员上场方案?
(2)如果在选出11名上场队员时,还要确定其中的守门员,那么教练员有多少种方式做这件事情?
C例2.在 100 件产品中,有 98 件合格品,2 件次品.从这 100 件产品中任意抽出 3 件 .
(1)有多少种不同的抽法?
(2)抽出的 3 件中恰好有 1 件是次品的抽法有多少种?
(3)抽出的 3 件中至少有 1 件是次品的抽法有多少种?
C变式:按下列条件,从12人中选出5人,有多少种不同选法?
(1)甲、乙、丙三人必须当选; (2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选; (4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选; (6)甲、乙、丙三人至少1人当选;
相关思维导图模板

树图思维导图提供 高二数学教案:组合(1) 在线思维导图免费制作,点击“编辑”按钮,可对 高二数学教案:组合(1) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c19911dd74eec817020802cbc2e6c6d1

树图思维导图提供 高二数学教案:组合(2) 在线思维导图免费制作,点击“编辑”按钮,可对 高二数学教案:组合(2) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:766bcd0b3d306852187a63dab9e44e51












 上海工商
上海工商