2019高考数学知识点:数列思维导图
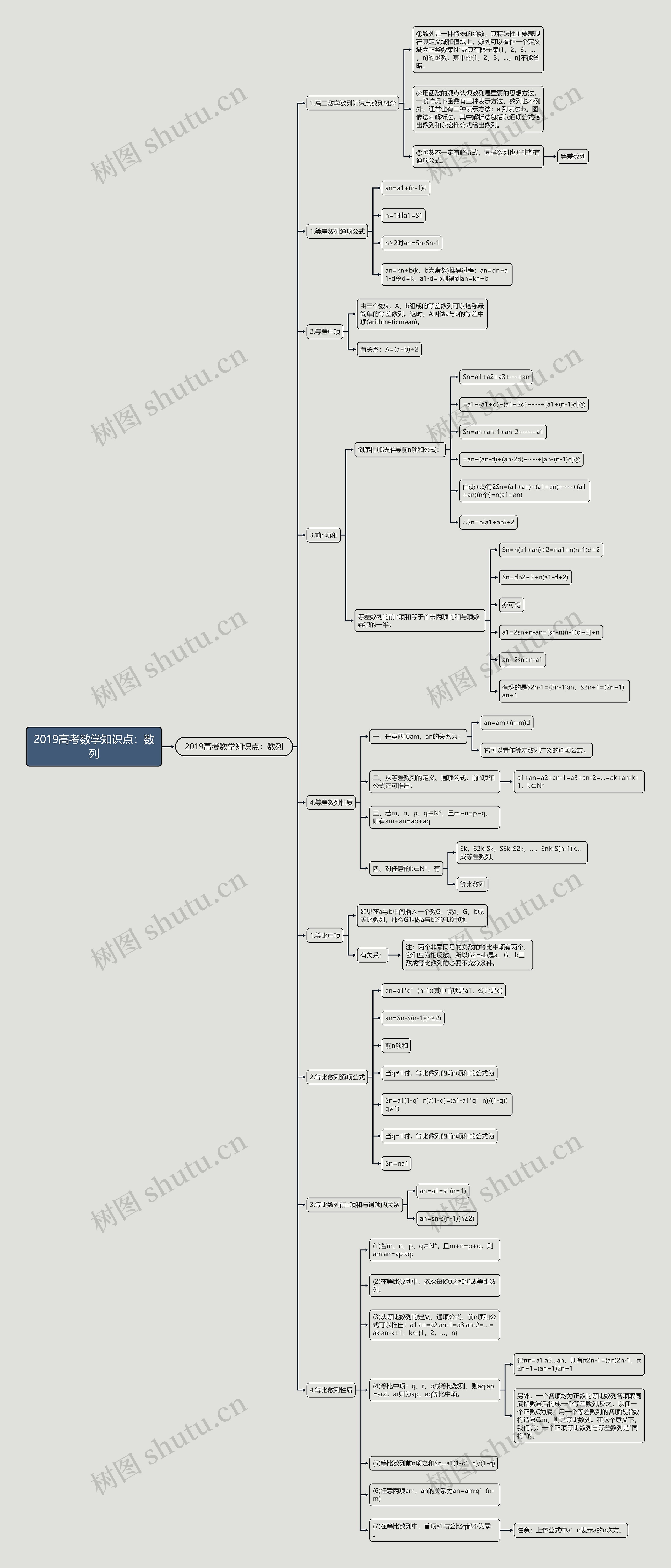
2019高考数学知识点:数列思维导图在高二数学中,数列概念是一种特殊的函数,其定义域和值域分别是正整数和实数集。数列有三种表示方法:列表法、图像法和解析法,解析法可以通过通项公式或递推公式来表示,等差数列是一种常见的数列类型,其通项公式为an=a1+(n-1)d,其中d为公差,a1为首项。等差数列中有一个特殊概念叫做等差中项,表示为A=(a+b)/2,其中a、A、b是等差数列的三个数。前n项和的推导公式为Sn=n(a1+an)/2,可以通过倒序相加法来推导,等差数列还有一些性质,如任意两项之间的关系、首尾项之和相等、等差数列之间的和相等。等差数列中的一些有趣关系,如S2n-1=(2n-1)an和S2n+1=(2n+1)an+1也是需要注意的内容。最后还有一个有趣的规律,Sk,S2k-Sk,S3k-S2k,…,Snk-S(n-1)k形成一个等差数列,以上就是2019高考数学知识点:数列思维导图中的知识点。
思维导图大纲
2019高考数学知识点:数列思维导图模板大纲
2019高考数学知识点:数列
1.高二数学数列知识点数列概念
①数列是一种特殊的函数。其特殊性主要表现在其定义域和值域上。数列可以看作一个定义域为正整数集N*或其有限子集{1,2,3,…,n}的函数,其中的{1,2,3,…,n}不能省略。
②用函数的观点认识数列是重要的思想方法,一般情况下函数有三种表示方法,数列也不例外,通常也有三种表示方法:a.列表法;b。图像法;c.解析法。其中解析法包括以通项公式给出数列和以递推公式给出数列。
③函数不一定有解析式,同样数列也并非都有通项公式。
等差数列
1.等差数列通项公式
an=a1+(n-1)d
n=1时a1=S1
n≥2时an=Sn-Sn-1
an=kn+b(k,b为常数)推导过程:an=dn+a1-d令d=k,a1-d=b则得到an=kn+b
2.等差中项
由三个数a,A,b组成的等差数列可以堪称最简单的等差数列。这时,A叫做a与b的等差中项(arithmeticmean)。
有关系:A=(a+b)÷2
3.前n项和
倒序相加法推导前n项和公式:
Sn=a1+a2+a3+·····+an
=a1+(a1+d)+(a1+2d)+······+[a1+(n-1)d]①
Sn=an+an-1+an-2+······+a1
=an+(an-d)+(an-2d)+······+[an-(n-1)d]②
由①+②得2Sn=(a1+an)+(a1+an)+······+(a1+an)(n个)=n(a1+an)
∴Sn=n(a1+an)÷2
等差数列的前n项和等于首末两项的和与项数乘积的一半:
Sn=n(a1+an)÷2=na1+n(n-1)d÷2
Sn=dn2÷2+n(a1-d÷2)
亦可得
a1=2sn÷n-an=[sn-n(n-1)d÷2]÷n
an=2sn÷n-a1
有趣的是S2n-1=(2n-1)an,S2n+1=(2n+1)an+1
4.等差数列性质
一、任意两项am,an的关系为:
an=am+(n-m)d
它可以看作等差数列广义的通项公式。
二、从等差数列的定义、通项公式,前n项和公式还可推出:
a1+an=a2+an-1=a3+an-2=…=ak+an-k+1,k∈N*
三、若m,n,p,q∈N*,且m+n=p+q,则有am+an=ap+aq
四、对任意的k∈N*,有
Sk,S2k-Sk,S3k-S2k,…,Snk-S(n-1)k…成等差数列。
等比数列
1.等比中项
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
有关系:
注:两个非零同号的实数的等比中项有两个,它们互为相反数,所以G2=ab是a,G,b三数成等比数列的必要不充分条件。
2.等比数列通项公式
an=a1*q’(n-1)(其中首项是a1,公比是q)
an=Sn-S(n-1)(n≥2)
前n项和
当q≠1时,等比数列的前n项和的公式为
Sn=a1(1-q’n)/(1-q)=(a1-a1*q’n)/(1-q)(q≠1)
当q=1时,等比数列的前n项和的公式为
Sn=na1
3.等比数列前n项和与通项的关系
an=a1=s1(n=1)
an=sn-s(n-1)(n≥2)
4.等比数列性质
(1)若m、n、p、q∈N*,且m+n=p+q,则am·an=ap·aq;
(2)在等比数列中,依次每k项之和仍成等比数列。
(3)从等比数列的定义、通项公式、前n项和公式可以推出:a1·an=a2·an-1=a3·an-2=…=ak·an-k+1,k∈{1,2,…,n}
(4)等比中项:q、r、p成等比数列,则aq·ap=ar2,ar则为ap,aq等比中项。
记πn=a1·a2…an,则有π2n-1=(an)2n-1,π2n+1=(an+1)2n+1
另外,一个各项均为正数的等比数列各项取同底指数幂后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,则是等比数列。在这个意义下,我们说:一个正项等比数列与等差数列是"同构"的。
(5)等比数列前n项之和Sn=a1(1-q’n)/(1-q)
(6)任意两项am,an的关系为an=am·q’(n-m)
(7)在等比数列中,首项a1与公比q都不为零。
注意:上述公式中a’n表示a的n次方。
相关思维导图模板

树图思维导图提供 2019高考数学知识点:等差数列求和 在线思维导图免费制作,点击“编辑”按钮,可对 2019高考数学知识点:等差数列求和 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6b0a07c76e49e54b9e9e0b23a171bb66

树图思维导图提供 2019高考数学必备知识点:数列的概念与简单表示法 在线思维导图免费制作,点击“编辑”按钮,可对 2019高考数学必备知识点:数列的概念与简单表示法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:dced923db644a3e93ee0a6bbe4ca7f85


















 上海工商
上海工商