2019高考数学知识点：等差数列求和思维导图

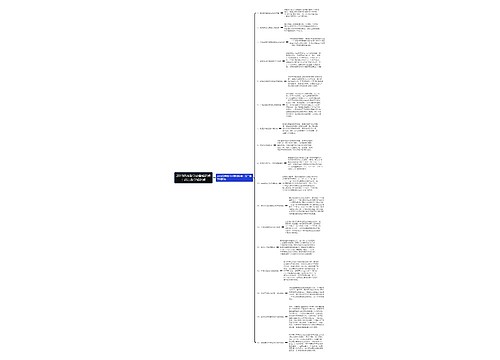
我来给你总结一下“2019高考数学知识点：等差数列求和思维导图”的知识点，等差数列求和公式是Sn=n(a1+an)/2，其中Sn表示前n项和，a1表示首项，an表示末项，n表示项数。还有另外一个等差数列求和公式Sn=na1+n(n-1)d/2=dn^2/2+(a1-d/2)n。

我们还需要了解一些等差数列的基本公式。末项等于首项加上(项数-1)乘以公差，项数于末项减去首项除以公差在加1，首项于末项减去(项数-1)乘以公差，总和等于首项加上末项在乘以项数除以2，末项表示等差数列的最后一位数，首项表示第一位数，项数表示等差数列中的总个数，和表示这些数的总和。

关于等差数列的推论，有几个重要的要点。从通项公式可以看出，a(n)是n的一次函数(d≠0)或常数函数(d=0)，这意味着(n，an)排在一条直线上，根据前n项和公式，S(n)是n的二次函数(d≠0)或一次函数(d=0，a1≠0)，且常数项为0。

根据等差数列的定义和通项公式，我们还可以推出：a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=…=a(k)+a(n-k+1)，其中k∈{1,2,…,n}。这个类似的规律也可以应用在其他数列上。

如果m，n，p，q属于自然数，满足m+n=p+q，那么有a(m)+a(n)=a(p)+a(q)，S(2n-1)=(2n-1)*a(n)，S(2n+1)=(2n+1)*a(n+1)，S(k)，S(2k)-S(k)，S(3k)-S(2k)，…，S(n)*k-S(n-1)*k…等都是等差数列。如果m+n=2p，则a(m)+a(n)=2*a(p)，这些推论的证明也是给出的。

等差数列求和的常用方法。分组求和是将一个数列分成几个可以直接求和的数列，拆项相消是将一个数列的通项公式分成两项差的形式，通过消去中间项，只剩下有限项在进行求和，错位相减是适用于一个等差数列和一个等比数列对应项相乘构成的数列求和的方法。还有倒序相加等，这些方法在解题过程中都会非常有用。

这些就是“2019高考数学知识点：等差数列求和思维导图”中的知识点。希望这样的口语化总结对你有帮助！