高考数学必修知识点总结思维导图
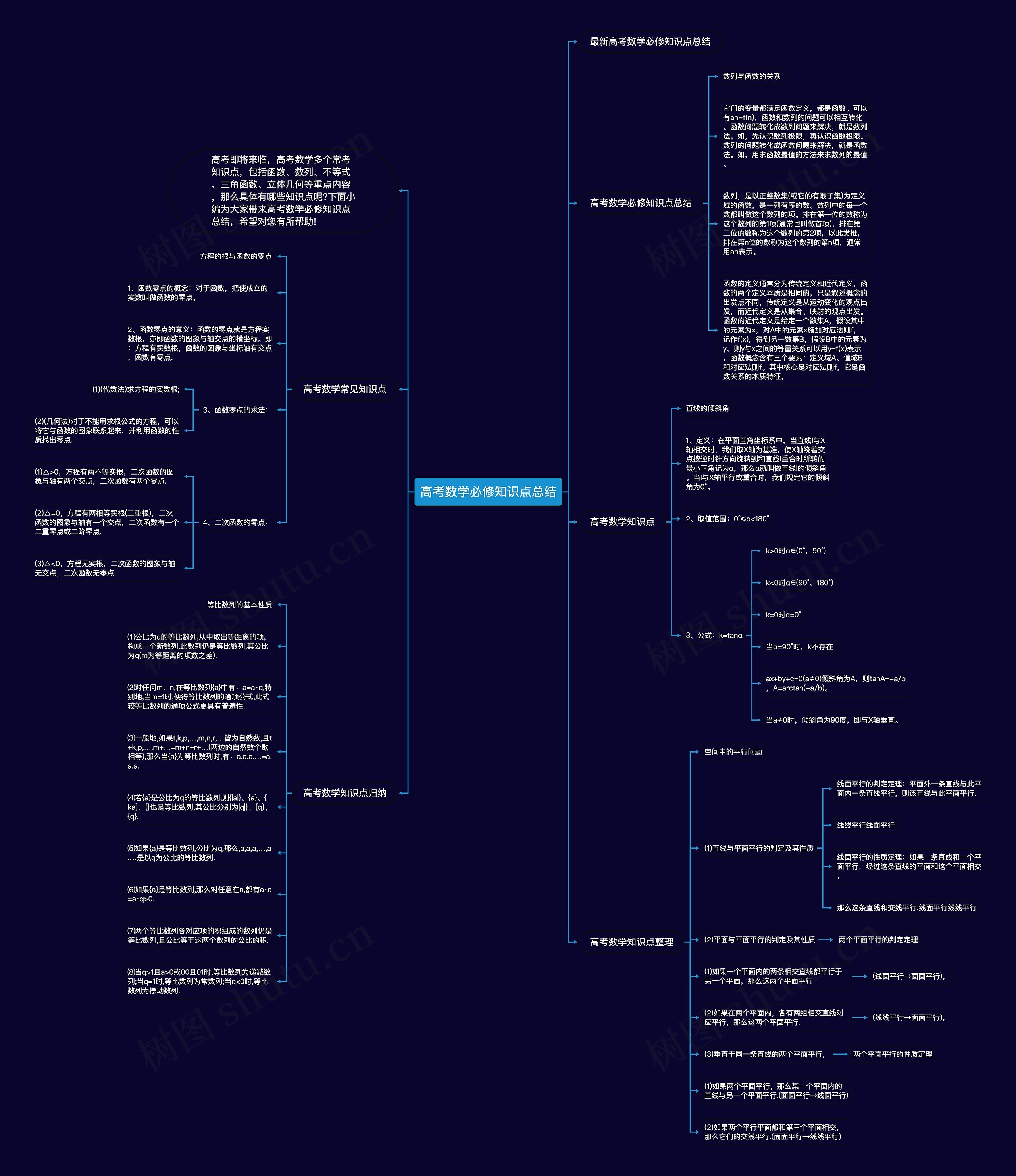
马上就要高考了,肯定要做好数学备考,数学中有很多重要的知识点需要掌握,包含函数、数列、不等式、三角函数和立体几何,如果想要更好的总结和记忆这些知识点,一个思维导图会非常有用,在导图上,你可以清晰地看到各个知识点的关系和重要概念。
我们来看数列与函数的关系。数列和函数都是满足函数定义的变量,可以用数列来解决函数问题,也可以用函数来解决数列问题,可以先了解数列的极限,在了解函数的极限,可以用求函数最值的方法来找到数列的最值。
数列是一列有序的数,其中每一个数称为数列的项。函数的定义根据传统定义和近代定义来分类,不管哪种定义,函数都有定义域、值域和对应法则这三个要素,其中对应法则是函数关系的核心特征。
高考数学中还有一些常见的内容,比如方程的根和函数的零点。函数的零点就是使函数成立的实数,也是方程的实数根,即函数图象和坐标轴的交点横坐标,可以通过代数法或几何法来求函数的零点,具体根据方程的类型选择合适的方法。
倾斜角是直线与X轴的夹角。在平面直角坐标系中,可以选择X轴作为基准,将其绕交点逆时针旋转到与直线重合的最小角度,这个角度就是直线的倾斜角。
希望这些高考数学必修知识点的总结对你有所帮助,加油!
思维导图大纲
高考数学必修知识点总结思维导图模板大纲
最新高考数学必修知识点总结
高考即将来临,高考数学多个常考知识点,包括函数、数列、不等式、三角函数、立体几何等重点内容,那么具体有哪些知识点呢?下面小编为大家带来高考数学必修知识点总结,希望对您有所帮助!
高考数学必修知识点总结
数列与函数的关系
它们的变量都满足函数定义,都是函数。可以有an=f(n),函数和数列的问题可以相互转化。函数问题转化成数列问题来解决,就是数列法。如,先认识数列极限,再认识函数极限。数列的问题转化成函数问题来解决,就是函数法。如,用求函数最值的方法来求数列的最值。
数列,是以正整数集(或它的有限子集)为定义域的函数,是一列有序的数。数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项(通常也叫做首项),排在第二位的数称为这个数列的第2项,以此类推,排在第n位的数称为这个数列的第n项,通常用an表示。
函数的定义通常分为传统定义和近代定义,函数的两个定义本质是相同的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。函数的近代定义是给定一个数集A,假设其中的元素为x,对A中的元素x施加对应法则f,记作f(x),得到另一数集B,假设B中的元素为y,则y与x之间的等量关系可以用y=f(x)表示,函数概念含有三个要素:定义域A、值域B和对应法则f。其中核心是对应法则f,它是函数关系的本质特征。
高考数学常见知识点
方程的根与函数的零点
1、函数零点的概念:对于函数,把使成立的实数叫做函数的零点。
2、函数零点的意义:函数的零点就是方程实数根,亦即函数的图象与轴交点的横坐标。即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.
3、函数零点的求法:
(1)(代数法)求方程的实数根;
(2)(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点.
4、二次函数的零点:
(1)△>0,方程有两不等实根,二次函数的图象与轴有两个交点,二次函数有两个零点.
(2)△=0,方程有两相等实根(二重根),二次函数的图象与轴有一个交点,二次函数有一个二重零点或二阶零点.
(3)△<0,方程无实根,二次函数的图象与轴无交点,二次函数无零点.
高考数学知识点
直线的倾斜角
1、定义:在平面直角坐标系中,当直线l与X轴相交时,我们取X轴为基准,使X轴绕着交点按逆时针方向旋转到和直线l重合时所转的最小正角记为α,那么α就叫做直线l的倾斜角。当l与X轴平行或重合时,我们规定它的倾斜角为0°。
2、取值范围:0°≤α<180°
3、公式:k=tanα
k>0时α∈(0°,90°)
k<0时α∈(90°,180°)
k=0时α=0°
当α=90°时,k不存在
ax+by+c=0(a≠0)倾斜角为A,则tanA=-a/b,A=arctan(-a/b)。
当a≠0时,倾斜角为90度,即与X轴垂直。
高考数学知识点归纳
等比数列的基本性质
⑴公比为q的等比数列,从中取出等距离的项,构成一个新数列,此数列仍是等比数列,其公比为q(m为等距离的项数之差).
⑵对任何m、n,在等比数列{a}中有:a=a·q,特别地,当m=1时,便得等比数列的通项公式,此式较等比数列的通项公式更具有普遍性.
⑶一般地,如果t,k,p,…,m,n,r,…皆为自然数,且t+k,p,…,m+…=m+n+r+…(两边的自然数个数相等),那么当{a}为等比数列时,有:a.a.a.…=a.a.a.
⑷若{a}是公比为q的等比数列,则{|a|}、{a}、{ka}、{}也是等比数列,其公比分别为|q|}、{q}、{q}.
⑸如果{a}是等比数列,公比为q,那么,a,a,a,…,a,…是以q为公比的等比数列.
⑹如果{a}是等比数列,那么对任意在n,都有a·a=a·q>0.
⑺两个等比数列各对应项的积组成的数列仍是等比数列,且公比等于这两个数列的公比的积.
⑻当q>1且a>0或00且01时,等比数列为递减数列;当q=1时,等比数列为常数列;当q<0时,等比数列为摆动数列.
高考数学知识点整理
空间中的平行问题
(1)直线与平面平行的判定及其性质
线面平行的判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.
线线平行线面平行
线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,
那么这条直线和交线平行.线面平行线线平行
(2)平面与平面平行的判定及其性质
两个平面平行的判定定理
(1)如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行
(线面平行→面面平行),
(2)如果在两个平面内,各有两组相交直线对应平行,那么这两个平面平行.
(线线平行→面面平行),
(3)垂直于同一条直线的两个平面平行,
两个平面平行的性质定理
(1)如果两个平面平行,那么某一个平面内的直线与另一个平面平行.(面面平行→线面平行)
(2)如果两个平行平面都和第三个平面相交,那么它们的交线平行.(面面平行→线线平行)
相关思维导图模板

树图思维导图提供 必修四数学知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 必修四数学知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:18b377b14a14f1e1442875b1daf48bae

树图思维导图提供 必修二数学知识点总结 在线思维导图免费制作,点击“编辑”按钮,可对 必修二数学知识点总结 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:32b43e2a9c0b8e73252719f6727eb6a4



















 上海工商
上海工商