第六章微分中值定理及其应用思维导图
树图思维导图提供 第六章微分中值定理及其应用 在线思维导图免费制作，点击“编辑”按钮，可对 第六章微分中值定理及其应用 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：7aa26cb90efd56e082376b40c89911c4
思维导图大纲
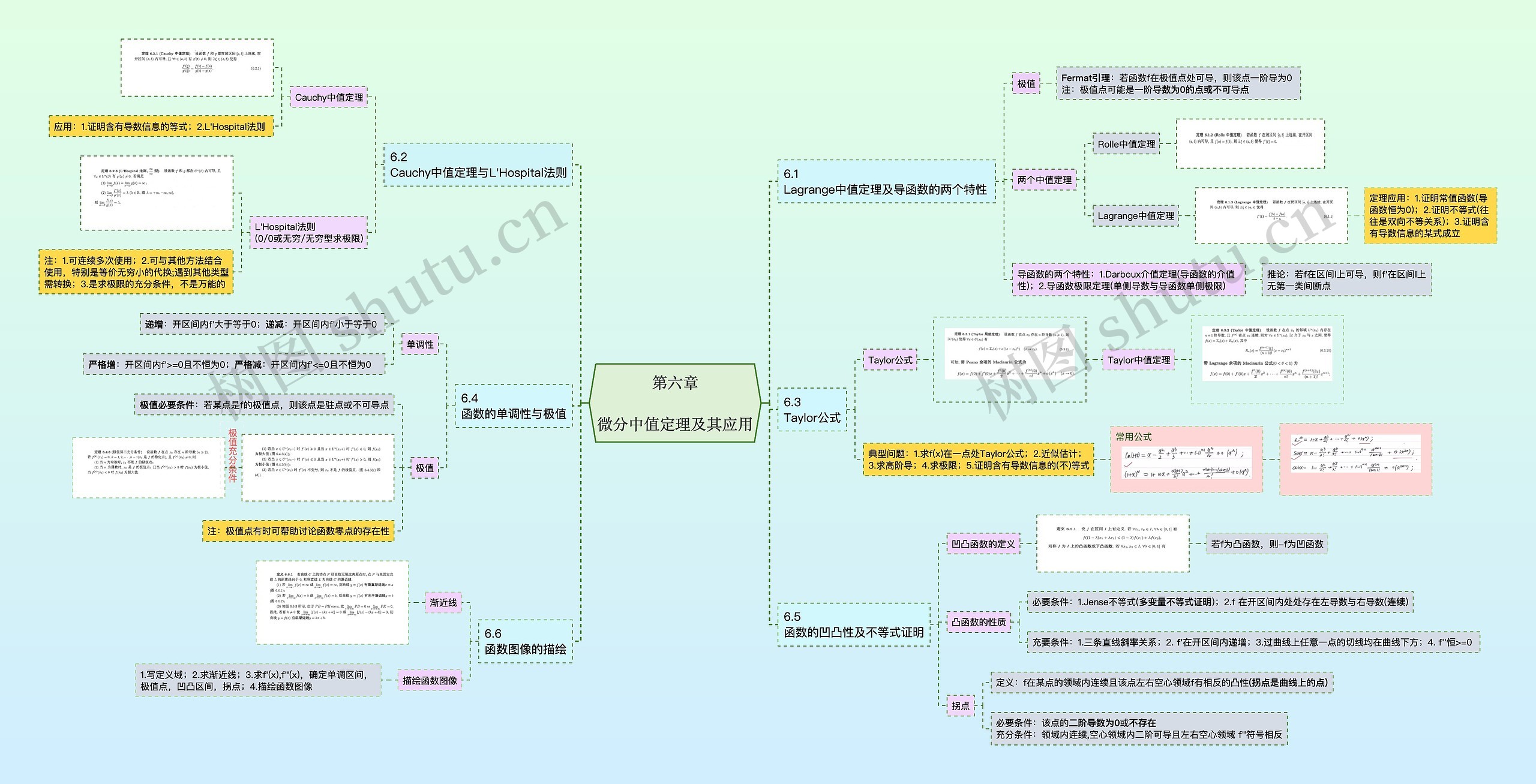
第六章 微分中值定理及其应用思维导图模板大纲
6.1 Lagrange中值定理及导函数的两个特性
极值
Fermat引理：若函数f在极值点处可导，则该点一阶导为0 注：极值点可能是一阶导数为0的点或不可导点
两个中值定理
Rolle中值定理
Lagrange中值定理
定理应用：1.证明常值函数(导函数恒为0)；2.证明不等式(往往是双向不等关系)；3.证明含有导数信息的某式成立
导函数的两个特性：1.Darboux介值定理(导函数的介值性)；2.导函数极限定理(单侧导数与导函数单侧极限)
推论：若f在区间I上可导，则f'在区间I上无第一类间断点
6.2 Cauchy中值定理与L'Hospital法则
Cauchy中值定理
应用：1.证明含有导数信息的等式；2.L'Hospital法则
L'Hospital法则 (0/0或无穷/无穷型求极限)
注：1.可连续多次使用；2.可与其他方法结合使用，特别是等价无穷小的代换;遇到其他类型需转换；3.是求极限的充分条件，不是万能的
6.3 Taylor公式
Taylor公式
Taylor中值定理
典型问题：1.求f(x)在一点处Taylor公式；2.近似估计；3.求高阶导；4.求极限；5.证明含有导数信息的(不)等式
常用公式
6.4 函数的单调性与极值
单调性
递增：开区间内f'大于等于0；递减：开区间内f'小于等于0
严格增：开区间内f'>=0且不恒为0；严格减：开区间内f'<=0且不恒为0
极值
极值必要条件：若某点是f的极值点，则该点是驻点或不可导点
注：极值点有时可帮助讨论函数零点的存在性
6.5 函数的凹凸性及不等式证明
凹凸函数的定义
若f为凸函数，则-f为凹函数
凸函数的性质
必要条件：1.Jense不等式(多变量不等式证明)；2.f 在开区间内处处存在左导数与右导数(连续)
充要条件：1.三条直线斜率关系；2. f'在开区间内递增；3.过曲线上任意一点的切线均在曲线下方；4. f''恒>=0
拐点
定义：f在某点的领域内连续且该点左右空心领域f有相反的凸性(拐点是曲线上的点)
必要条件：该点的二阶导数为0或不存在 充分条件：领域内连续,空心领域内二阶可导且左右空心领域 f''符号相反
6.6 函数图像的描绘
渐近线
描绘函数图像
1.写定义域；2.求渐近线；3.求f'(x),f''(x)，确定单调区间，极值点，凹凸区间，拐点；4.描绘函数图像
极值充分条件思维导图模板大纲
沪公网安备 31011502019485号
上海工商