椭圆的第二定义 内容是什么思维导图
免费下载
免费使用文件
心不动则不痛 浏览量:72023-01-12 15:37:09
已被使用0次
平面上到定点F的距离与到定直线的距离之比为常数e(即椭圆的离心率,e=c/a)的点的集合(定点F不在定直线上,该常数为小于1的正数)。
树图思维导图提供 椭圆的第二定义 内容是什么 在线思维导图免费制作,点击“编辑”按钮,可对 椭圆的第二定义 内容是什么 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:069bd8a25392e3763dac59fc721c9228
思维导图大纲
椭圆的第二定义 内容是什么思维导图模板大纲
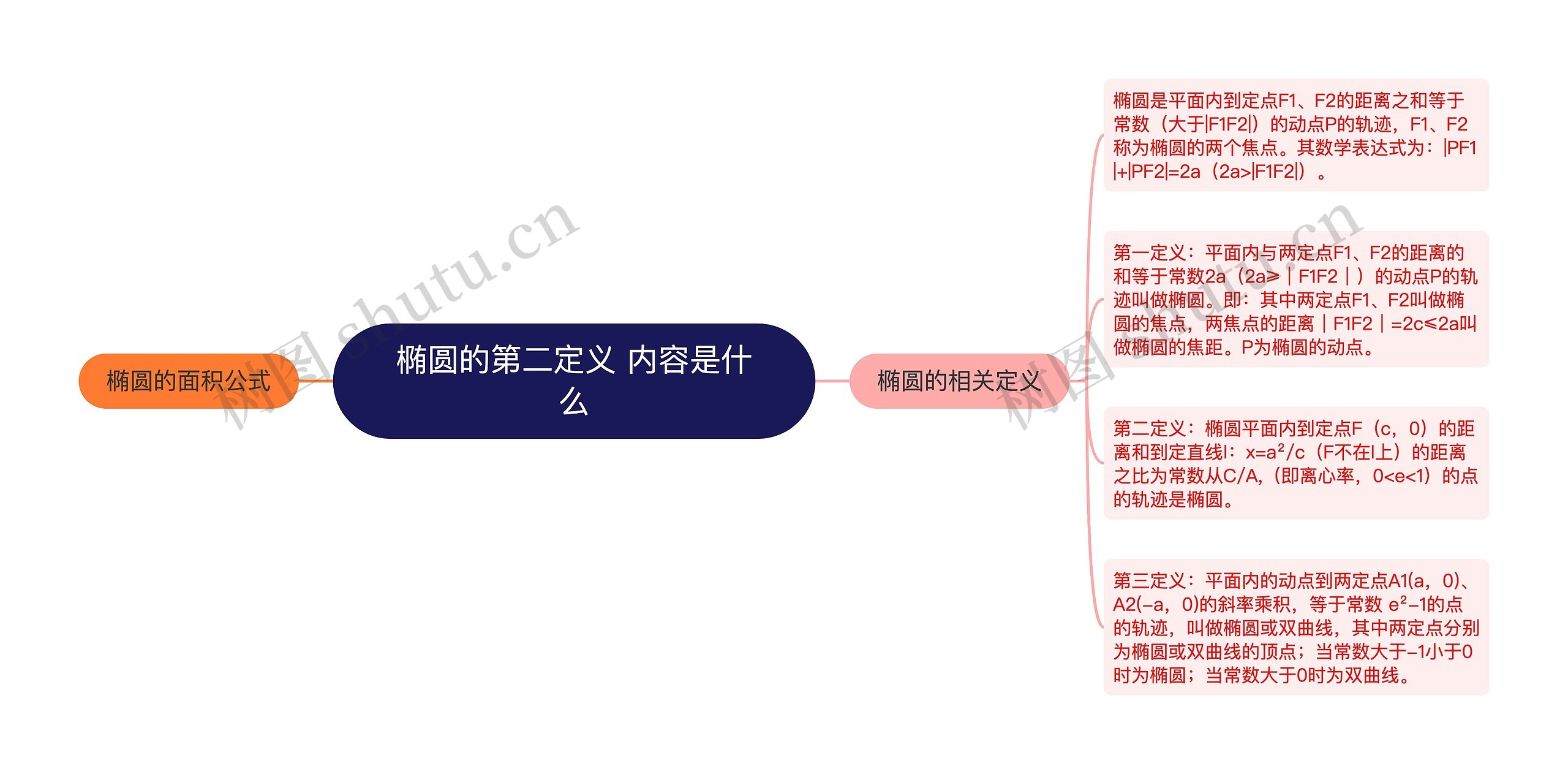
椭圆的相关定义
椭圆是平面内到定点F1、F2的距离之和等于常数(大于|F1F2|)的动点P的轨迹,F1、F2称为椭圆的两个焦点。其数学表达式为:|PF1|+|PF2|=2a(2a>|F1F2|)。
第一定义:平面内与两定点F1、F2的距离的和等于常数2a(2a≥|F1F2|)的动点P的轨迹叫做椭圆。即:其中两定点F1、F2叫做椭圆的焦点,两焦点的距离|F1F2|=2c≤2a叫做椭圆的焦距。P为椭圆的动点。
第二定义:椭圆平面内到定点F(c,0)的距离和到定直线l:x=a²/c(F不在l上)的距离之比为常数从C/A,(即离心率,0<e<1)的点的轨迹是椭圆。
第三定义:平面内的动点到两定点A1(a,0)、A2(-a,0)的斜率乘积,等于常数 e²-1的点的轨迹,叫做椭圆或双曲线,其中两定点分别为椭圆或双曲线的顶点;当常数大于-1小于0时为椭圆;当常数大于0时为双曲线。
椭圆的面积公式












 上海工商
上海工商