兀是无理数还是有理数怎么证明思维导图
π是无理数。因为，根据有理数的定义：有理数是一个整数a和一个正整数b的比，例如3/8，通则为a/b。有理数的小数部分是有限或为无限循环的数。而π=3.1415926...是无限不循环小数，不在有理数的范围。
树图思维导图提供 兀是无理数还是有理数怎么证明 在线思维导图免费制作，点击“编辑”按钮，可对 兀是无理数还是有理数怎么证明 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：63f3b8ceb95e13d1c92e2e755ccc7e6a
思维导图大纲
兀是无理数还是有理数怎么证明思维导图模板大纲
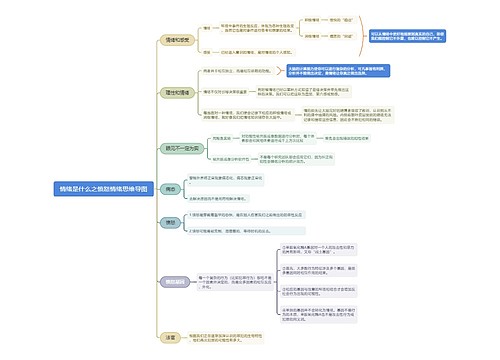
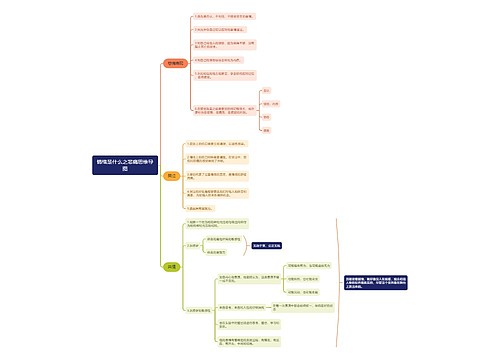
证明过程
令f(x)=(x^n)[(a-bx)^n]/(n!)
若0<x<a/b,则
0<f(x)<(π^n)(a^n)/(n!)
0<sinx<1
以上两式相乘得：
0<f(x)sinx<(π^n)(a^n)/(n!)
当n充分大时，,在[0，π]区间上的积分有
0<∫f(x)sinxdx <[π^(n+1)](a^n)/(n!)<1 …………（1）
又令：F(x)=f(x)-f"(x)+[f(x)]^(4)-…+[(-1)^n][f(x)]^(2n),(表示偶数阶导数)
由于n!f(x)是x的整系数多项式，且各项的次数都不小于n，故f(x)及其各阶导数在x=0点处的值也都是整数，因此，F(x)和F(π)也都是整数。
又因为
d[F'(x)sinx-F(x)conx]/dx
=F"(x)sinx+F'(x)cosx-F'(x)cosx+F(x)sinx
=F"(x)sinx+F(x)sinx
=f(x)sinx
所以有：
∫f(x)sinxdx=[F'(x)sinx-F(x)cosx]，（此处上限为π，下限为0）
=F(π)+F(0)
上式表示∫f(x)sinxdx在[0，π]区间上的积分为整数，这与（1）式矛盾。所以π不是有理数，又它是实数，故π是无理数。
圆周率
相关思维导图模板
树图思维导图提供 影子还可以怎么玩 在线思维导图免费制作，点击“编辑”按钮，可对 影子还可以怎么玩 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：4d614e09bfb803c46b43c88c3b44bc79
树图思维导图提供 八年级物理（第三单元） 在线思维导图免费制作，点击“编辑”按钮，可对 八年级物理（第三单元） 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：13a65c3defeb87004aa1c7c846526ef1
沪公网安备 31011502019485号
上海工商