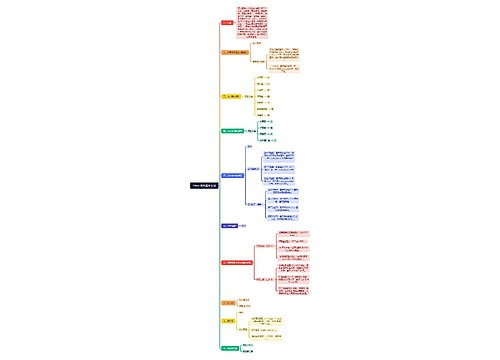
二阶常系数齐次线性微分方程 特解y*设法思维导图

树图思维导图提供 二阶常系数齐次线性微分方程 特解y*设法 在线思维导图免费制作,点击“编辑”按钮,可对 二阶常系数齐次线性微分方程 特解y*设法 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7533fdb5397bd51870621b94e6008685
思维导图大纲
二阶常系数齐次线性微分方程 特解y*设法思维导图模板大纲
一,二阶常系数齐次线性微分方程
标准形式
y″+py′+qy=0
特征方程
r^2+pr+q=0
通解
1.两个不相等的实根:y=C1e^(r1x)+C2e^(r2x)
2.两根相等的实根:y=(C1+C2x)e^(r1x)
3.一对共轭复根:r1=α+iβ,r2=α-iβ:y=e^(αx)*(C1cosβx+C2sinβx)
二,特解y*设法
1、如果f(x)=P(x),Pn(x)为n阶多项式。
若0不是特征值,在令特解y*=x^k*Qm(x)*e^λx中,k=0,λ=0;因为Qm(x)与Pn(x)为同次的多项式,所以Qm(x)设法要根据Pn(x)的情况而定。
比如如果Pn(x)=a(a为常数),则设Qm(x)=A(A为另一个未知常数);如果Pn(x)=x,则设Qm(x)=ax+b;如果Pn(x)=x^2,则设Qm(x)=ax^2+bx+c。
若0是特征方程的单根,在令特解y*=x^k*Qm(x)*e^λx中,k=1,λ=0,即y*=x*Qm(x)。
若0是特征方程的重根,在令特解y*=x^k*Qm(x)*e^λx中,k=2,λ=0,即y*=x^2*Qm(x)。
2、如果f(x)=P(x)e^αx,Pn(x)为n阶多项式。
若α不是特征值,在令特解y*=x^k*Qm(x)*e^αx中,k=0,即y*=Qm(x)*e^αx,Qm(x)设法要根据Pn(x)的情况而定。
若α是特征方程的单根,在令特解y*=x^k*Qm(x)*e^αx中,k=1,即y*=x*Qm(x)*e^αx。
若α是特征方程的重根,在令特解y*=x^k*Qm(x)*e^λx中,k=2,即y*=x^2*Qm(x)*e^αx。
3、如果f(x)=[Pl(x)cos(βx)+Pn(x)sin(βx)]e^αx,Pl(x)为l阶多项式,Pn(x)为n阶多项式。
若α±iβ不是特征值,在令特解y*=x^k*[Rm1(x)cos(βx)+Rm2(x)sin(βx)]e^αx中,k=0,m=max{l,n},Rm1(x)与Rm2(x)设法要根据Pl(x)或Pn(x)的情况而定(同Qm(x)设法要根据Pn(x)的情况而定的原理一样)。
即y*=[Rm1(x)cos(βx)+Rm2(x)sin(βx)]e^αx
若α±iβ不是特征值,在令特解y*=x^k*[Rm1(x)cos(βx)+Rm2(x)sin(βx)]e^αx中,k=1,即y*=x*[Rm1(x)cos(βx)+Rm2(x)sin(βx)]e^αx。
相关思维导图模板

树图思维导图提供 Linux 网络基础知识 在线思维导图免费制作,点击“编辑”按钮,可对 Linux 网络基础知识 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:199680f0e48eac8a1aeaadb90447d4f4


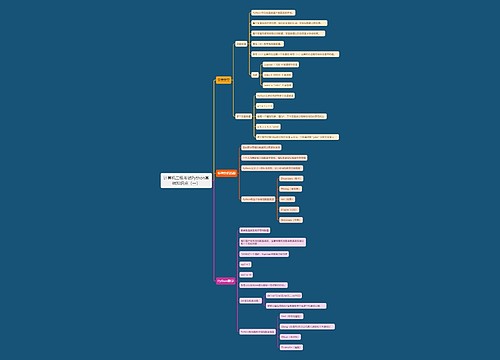
树图思维导图提供 ——重点行业机构业务客户生态图谱(锦州地区) 在线思维导图免费制作,点击“编辑”按钮,可对 ——重点行业机构业务客户生态图谱(锦州地区) 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f930058a554a09639a5c5c0e168c451c






 上海工商
上海工商