高等数学之线代行列式思维导图
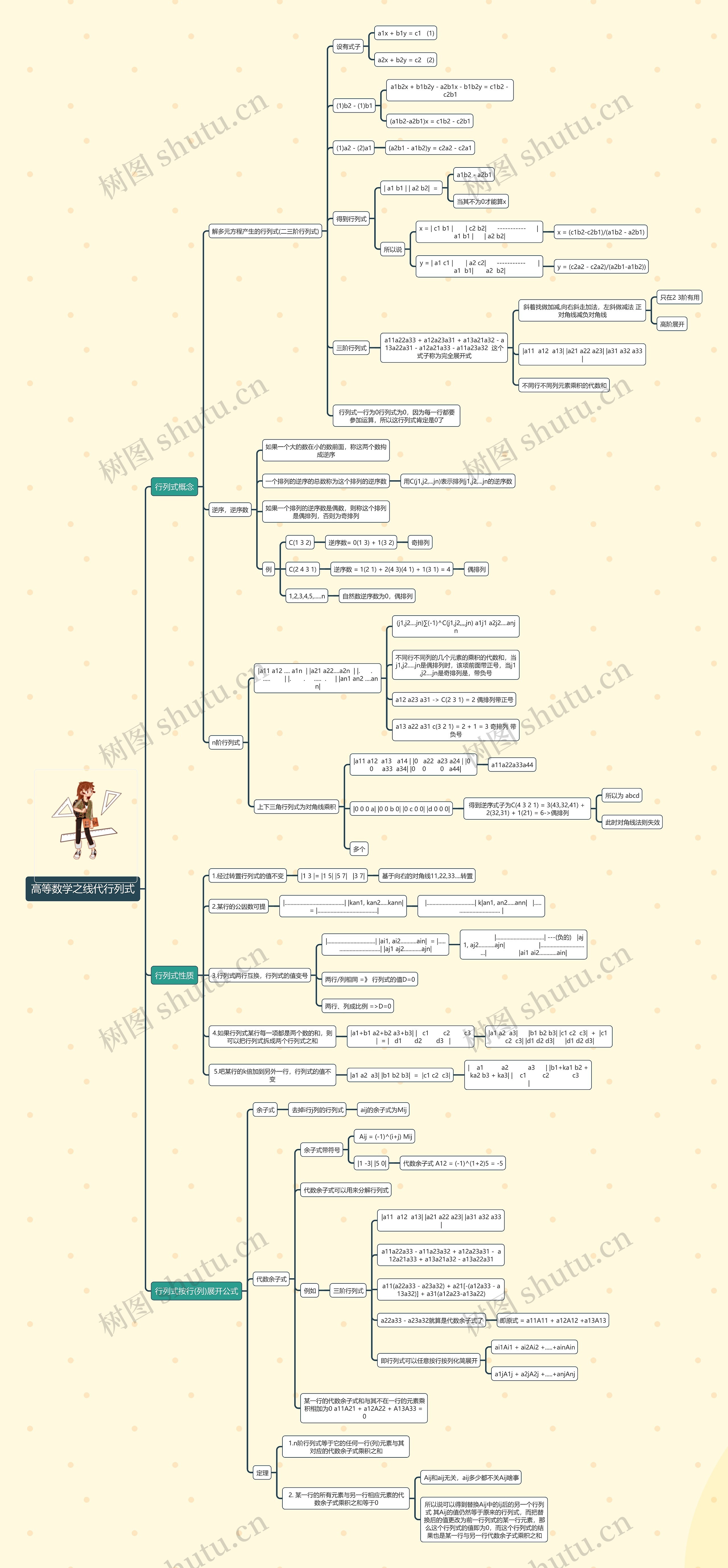
介绍高等数学之线代行列式
树图思维导图提供 高等数学之线代行列式 在线思维导图免费制作,点击“编辑”按钮,可对 高等数学之线代行列式 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:66b0d473c5cf57ecdc208665057d9776
思维导图大纲
高等数学之线代行列式思维导图模板大纲
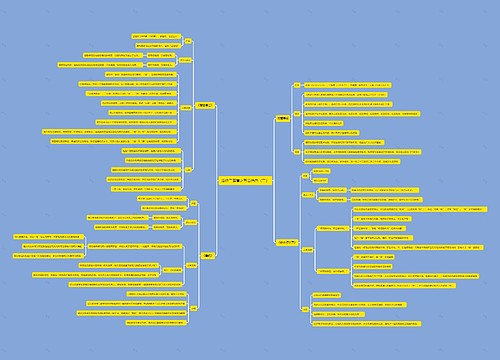
行列式概念
解多元方程产生的行列式(二三阶行列式)
设有式子
a1x + b1y = c1 (1)
a2x + b2y = c2 (2)
(1)b2 - (1)b1
a1b2x + b1b2y - a2b1x - b1b2y = c1b2 - c2b1
(a1b2-a2b1)x = c1b2 - c2b1
(1)a2 - (2)a1
(a2b1 - a1b2)y = c2a2 - c2a1
得到行列式
| a1 b1 | | a2 b2| =
a1b2 - a2b1
当其不为0才能算x
所以说
x = | c1 b1 | | c2 b2| ----------- | a1 b1 | | a2 b2|
x = (c1b2-c2b1)/(a1b2 - a2b1)
y = | a1 c1 | | a2 c2| ----------- |a1 b1| a2 b2|
y = (c2a2 - c2a2)/(a2b1-a1b2))
三阶行列式
a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32 这个式子称为完全展开式
斜着找做加减,向右斜走加法,左斜做减法 正对角线减负对角线
只在2 3阶有用
高阶展开
|a11 a12 a13| |a21 a22 a23| |a31 a32 a33|
不同行不同列元素乘积的代数和
行列式一行为0行列式为0,因为每一行都要参加运算,所以这行列式肯定是0了
逆序,逆序数
如果一个大的数在小的数前面,称这两个数构成逆序
一个排列的逆序的总数称为这个排列的逆序数
用C(j1,j2,...jn)表示排列j1,j2,...jn的逆序数
如果一个排列的逆序数是偶数,则称这个排列是偶排列,否则为奇排列
例
C(1 3 2)
逆序数= 0(1 3) + 1(3 2)
奇排列
C(2 4 3 1)
逆序数 = 1(2 1) + 2(4 3)(4 1) + 1(3 1) = 4
偶排列
1,2,3,4,5,.....n
自然数逆序数为0,偶排列
n阶行列式
|a11 a12 .... a1n | |a21 a22....a2n | |. . ..... | |. . ..... . | |an1 an2 ....ann|
(j1,j2....jn)∑(-1)^C(j1,j2,,,,jn) a1j1 a2j2....anjn
不同行不同列的几个元素的乘积的代数和,当j1,j2.....jn是偶排列时,该项前面带正号,当j1,j2....jn是奇排列是,带负号
a12 a23 a31 -> C(2 3 1) = 2 偶排列带正号
a13 a22 a31 c(3 2 1) = 2 + 1 = 3 奇排列 带负号
上下三角行列式为对角线乘积
|a11 a12 a13 a14 | |0 a22 a23 a24 | |0 0 a33 a34| |0 0 0 a44|
a11a22a33a44
|0 0 0 a| |0 0 b 0| |0 c 0 0| |d 0 0 0|
得到逆序式子为C(4 3 2 1) = 3(43,32,41) + 2(32,31) + 1(21) = 6->偶排列
所以为 abcd
此时对角线法则失效
多个
行列式性质
1.经过转置行列式的值不变
|1 3 |= |1 5| |5 7| |3 7|
基于向右的对角线11,22,33....转置
2.某行的公因数可提
|.........................................| |kan1, kan2.....kann| = |.........................................|
|.................................| k|an1, an2.....ann| |................................. |
3.行列式两行互换,行列式的值变号
|.................................| |ai1, ai2...........ain| = |.................................| |aj1 aj2............ajn|
|.................................| ---(负的) |aj1, aj2...........ajn| |.................................| |ai1 ai2............ain|
两行/列相同 =》 行列式的值D=0
两行、列成比例 =>D=0
4.如果行列式某行每一项都是两个数的和,则可以把行列式拆成两个行列式之和
|a1+b1 a2+b2 a3+b3| | c1 c2 c3 | = | d1 d2 d3 |
|a1 a2 a3| |b1 b2 b3| |c1 c2 c3| + |c1 c2 c3| |d1 d2 d3| |d1 d2 d3|
5.吧某行的k倍加到另外一行,行列式的值不变
|a1 a2 a3| |b1 b2 b3| = |c1 c2 c3|
| a1 a2 a3 | |b1+ka1 b2 + ka2 b3 + ka3| | c1 c2 c3 |
行列式按行(列)展开公式
余子式
去掉i行j列的行列式
aij的余子式为Mij
代数余子式
余子式带符号
Aij = (-1)^(i+j) Mij
|1 -3| |5 0|
代数余子式 A12 = (-1)^(1+2)5 = -5
代数余子式可以用来分解行列式
例如
三阶行列式
|a11 a12 a13| |a21 a22 a23| |a31 a32 a33|
a11a22a33 - a11a23a32 + a12a23a31 - a12a21a33 + a13a21a32 - a13a22a31
a11(a22a33 - a23a32) + a21[-(a12a33 - a13a32)] + a31(a12a23-a13a22)
a22a33 - a23a32就算是代数余子式了
即原式 = a11A11 + a12A12 +a13A13
即行列式可以任意按行按列化简展开
ai1Ai1 + ai2Ai2 +.....+ainAin
a1jA1j + a2jA2j +.....+anjAnj
某一行的代数余子式和与其不在一行的元素乘积相加为0 a11A21 + a12A22 + A13A33 = 0
定理
1.n阶行列式等于它的任何一行(列)元素与其对应的代数余子式乘积之和
2. 某一行的所有元素与另一行相应元素的代数余子式乘积之和等于0
Aij和aij无关,aij多少都不关Aij啥事
所以说可以得到替换Aij中的ij后的另一个行列式 其Aij的值仍然等于原来的行列式,而把替换后的值更改为前一行列式的某一行元素,那么这个行列式的值即为0,而这个行列式的结果也是某一行与另一行代数余子式乘积之和
思维导图模板大纲
相关思维导图模板

树图思维导图提供 高等数学之线代矩阵 在线思维导图免费制作,点击“编辑”按钮,可对 高等数学之线代矩阵 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:93284208ca082afc81d3effb01247f3f


树图思维导图提供 大学数学教学工作总结范文 在线思维导图免费制作,点击“编辑”按钮,可对 大学数学教学工作总结范文 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:5c571ad28f498dcf4b30cec66a515770







 上海工商
上海工商