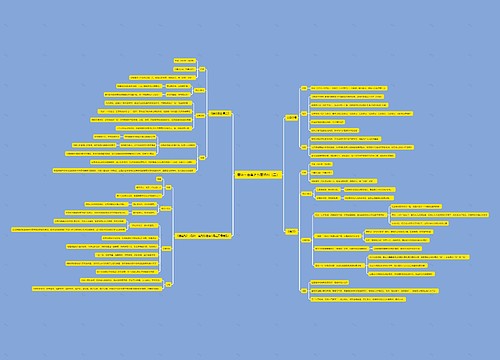
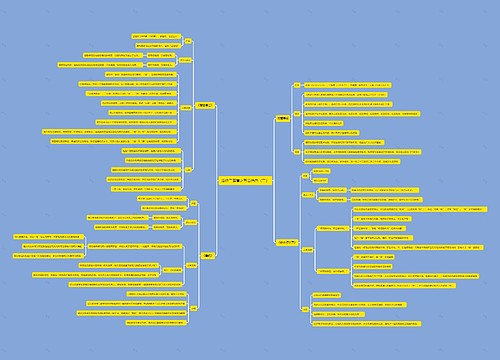
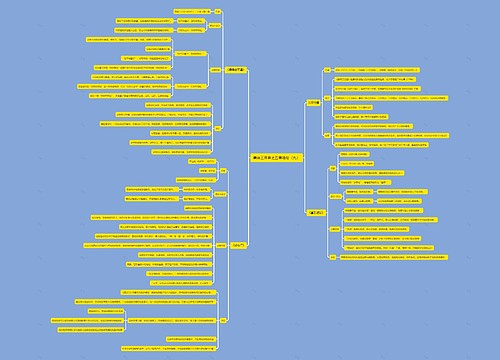
高等数学之线代矩阵思维导图
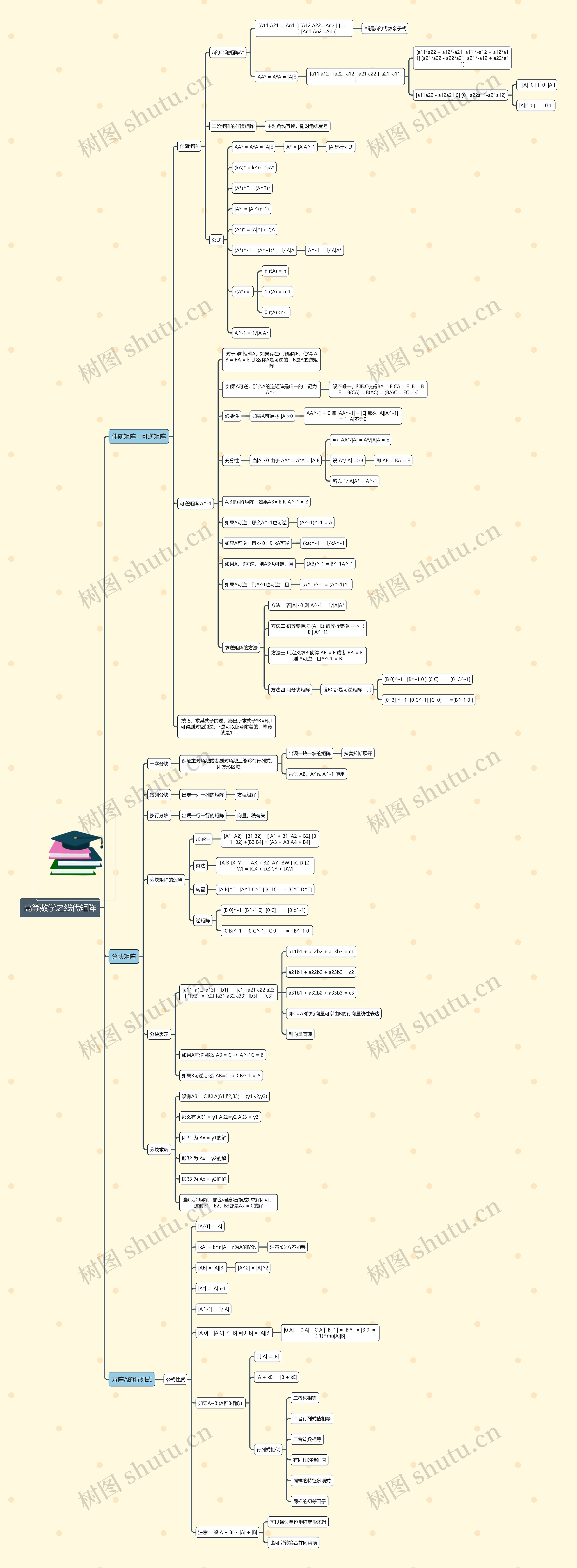
高等数学之线代矩阵思维导图涵盖了伴随矩阵、可逆矩阵等,伴随矩阵可用于计算矩阵的逆,且具有一些性质,如伴随矩阵的转置等于其自身,可逆矩阵是指存在逆矩阵的矩阵,且逆矩阵唯一,对于某些矩阵,如分块矩阵,可使用运算规则,如加减法、乘法、转置和逆矩阵。简化计算,本模板还介绍了求解逆矩阵的几种方法,例如初等变换法和分块矩阵法,方阵的行列式性质,例如行列式相似、有同样的特征多项式和初等因子。
思维导图大纲
高等数学之线代矩阵思维导图模板大纲
伴随矩阵,可逆矩阵
伴随矩阵
A的伴随矩阵A*
[A11 A21 .....An1 ] [A12 A22... An2 ] [.... ] [An1 An2....Ann]
Aij是A的代数余子式
AA* = A*A = |A|E
[a11 a12 ] [a22 -a12] [a21 a22][-a21 a11 ]
[a11*a22 + a12*-a21 a11 *-a12 + a12*a11] [a21*a22 - a22*a21 a21*-a12 + a22*a11]
[a11a22 - a12a21 0] [0 a22a11-a21a12]
[ |A| 0 ] [ 0 |A|]
|A|[1 0] [0 1]
二阶矩阵的伴随矩阵
主对角线互换,副对角线变号
公式
AA* = A*A = |A|E
A* = |A|A^-1
|A|是行列式
(kA)* = k^(n-1)A*
(A*)^T = (A^T)*
|A*| = |A|^(n-1)
(A*)* = |A|^(n-2)A
(A*)^-1 = (A^-1)* = 1/|A|A
A^-1 = 1/|A|A*
r(A*) =
n r(A) = n
1 r(A) = n-1
0 r(A)<n-1
A^-1 = 1/|A|A*
可逆矩阵 A^-1
对于n阶矩阵A,如果存在n阶矩阵B,使得 AB = BA = E, 那么称A是可逆的,B是A的逆矩阵
如果A可逆,那么A的逆矩阵是唯一的,记为A^-1
设不唯一,即B,C使得BA = E CA = E B = BE = B(CA) = B(AC) = (BA)C = EC = C
必要性
如果A可逆-》|A|≠0
AA^-1 = E 即 |AA^-1| = |E| 那么 |A||A^-1| = 1 |A|不为0
充分性
当|A|≠0 由于 AA* = A*A = |A|E
=> AA*/|A| = A*/|A|A = E
设 A*/|A| =>B
即 AB = BA = E
所以 1/|A|A* = A^-1
A,B是n阶矩阵,如果AB= E 则A^-1 = B
如果A可逆,那么A^-1也可逆
(A^-1)^-1 = A
如果A可逆,且k≠0,则kA可逆
(ka)^-1 = 1/kA^-1
如果A,B可逆,则AB也可逆,且
(AB)^-1 = B^-1A^-1
如果A可逆,则A^T也可逆,且
(A^T)^-1 = (A^-1)^T
求逆矩阵的方法
方法一 若|A|≠0 则 A^-1 = 1/|A|A*
方法二 初等变换法 (A | E) 初等行变换 ---> (E | A^-1)
方法三 用定义求B 使得 AB = E 或者 BA = E 则 A可逆,且A^-1 = B
方法四 用分块矩阵
设BC都是可逆矩阵,则
[B 0]^-1 [B^-1 0 ] [0 C] = [0 C^-1]
[0 B] ^ -1 [0 C^-1] [C 0] =[B^-1 0 ]
技巧,求某式子的逆,凑出所求式子*B=E即可得到对应的逆,E是可以随意附着的,毕竟就是1
分块矩阵
十字分块
保证主对角线或者副对角线上能够有行列式,即方形区域
出现一块一块的矩阵
拉普拉斯展开
乘法 AB,A^n, A^-1 使用
按列分块
出现一列一列的矩阵
方程组解
按行分块
出现一行一行的矩阵
向量,秩有关
分块矩阵的运算
加减法
[A1 A2] [B1 B2] [ A1 + B1 A2 + B2] [B1 B2] +[B3 B4] = [A3 + A3 A4 + B4]
乘法
[A B][X Y ] [AX + BZ AY+BW ] [C D][Z W] = [CX + DZ CY + DW]
转置
[A B]^T [A^T C^T ] [C D] = [C^T D^T]
逆矩阵
[B 0]^-1 [B^-1 0] [0 C] = [0 c^-1]
[0 B]^-1 [0 C^-1] [C 0] = [B^-1 0]
分块表示
[a11 a12 a13] [b1] [c1] [a21 a22 a23] *[b2] = [c2] [a31 a32 a33] [b3] [c3]
a11b1 + a12b2 + a13b3 = c1
a21b1 + a22b2 + a23b3 = c2
a31b1 + a32b2 + a33b3 = c3
即C=AB的行向量可以由B的行向量线性表达
列向量同理
如果A可逆 那么 AB = C -> A^-1C = B
如果B可逆 那么 AB=C -> CB^-1 = A
分块求解
设有AB = C 即 A(ß1,ß2,ß3) = (γ1,γ2,γ3)
那么有 Aß1 = γ1 Aß2=γ2 Aß3 = γ3
即ß1 为 Ax = γ1的解
即ß2 为 Ax = γ2的解
即ß3 为 Ax = γ3的解
当C为0矩阵,那么γ全部替换成0求解即可,这时ß1,ß2,ß3都是Ax = 0的解
方阵A的行列式
公式性质
|A^T| = |A|
|kA| = k^n|A| n为A的阶数
注意n次方不能丢
|AB| = |A||B|
|A^2| = |A|^2
|A*| = |A|n-1
|A^-1| = 1/|A|
|A 0| |A C| |* B| =|0 B| = |A||B|
|0 A| |0 A| |C A | |B * | = |B * | = |B 0| = (-1)^mn|A||B|
如果A~B (A和B相似)
则|A| = |B|
|A + kE| = |B + kE|
行列式相似
二者秩相等
二者行列式值相等
二者迹数相等
有同样的特征值
同样的特征多项式
同样的初等因子
注意 一般|A + B| ≠ |A| + |B|
可以通过单位矩阵变形求得
也可以转换合并同类项
思维导图模板大纲
相关思维导图模板
树图思维导图提供 考研数学三知识点总结思维导图 在线思维导图免费制作,点击“编辑”按钮,可对 考研数学三知识点总结思维导图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7e481da9e8f11a2c076a54af60307129
树图思维导图提供 考研数学必备知识点总结思维导图 在线思维导图免费制作,点击“编辑”按钮,可对 考研数学必备知识点总结思维导图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0ba99b31b57b5e7fa402c4c2df267175





 上海工商
上海工商