2022国考行测备考:数量关系之工程问题统筹类思维导图

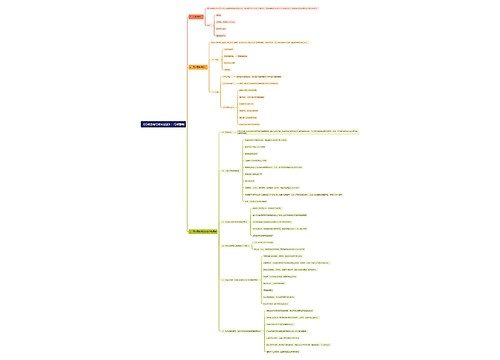
对于数量关系统筹类问题,考试共会出现以下两种形式,分别是时间型和效率型,接下来我们逐一分析。
树图思维导图提供 2022国考行测备考:数量关系之工程问题统筹类 在线思维导图免费制作,点击“编辑”按钮,可对 2022国考行测备考:数量关系之工程问题统筹类 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:505dcd48be5e2b93f5b66588741410a0
思维导图大纲
2022国考行测备考:数量关系之工程问题统筹类思维导图模板大纲
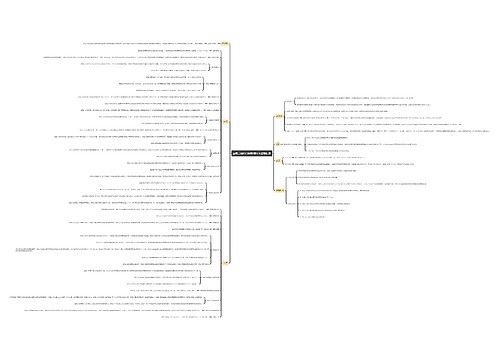
各位正在备考的小伙伴,今天我们来学习行测考试数量关系工程问题中大家比较纠结的一类题型,工程问题之统筹类。比如题干给了甲乙两人完成A、B两个项目分别需要多少天或甲乙两人完成A、B两项工程的效率分别为多少,问我们完成这项工程最少需要花多少天?解决这一类问题的核心难点也就在于怎么安排谁做哪一份工作,那么我们接下来通过一个小故事来分析一下。
小学我们学习过龟兔赛跑的故事,那么现在大家首先思考一个,现在如果要举办运动会,有长跑和游泳两个项目,现在如果要问你兔子和乌龟应该分别安排什么项目呢?是不是大家都会安排他们参加各自擅长的项目啊!那么对于我们数量关系统筹类的题目,也是这样一个逻辑,安排他们参加自己更加擅长的工作即可,也就是分析出自己更擅长于哪个项目即可!
对于数量关系统筹类问题,考试共会出现以下两种形式,分别是时间型和效率型,接下来我们逐一分析。
对于甲来说,完成A、B两个项目的时间之比为12:4=3:1;对于乙来说,完成A、B两个项目的时间之比为15:3=5:1。完成一个项目时间越小越快完成,(3:1)<(5:1),因此安排甲完成A项目,安排乙完成B项目。
对于甲来说,完成A、B两个项目的效率之比为12:4=3:1;对于乙来说,完成A、B两个项目的效率之比为15:3=5:1。完成一个项目效率越大越快完成,(5:1)>(3:1),因此安排乙完成A项目,甲完成B项目。
以上就是数量关系考试中工程统筹问题中的两种出题方式,接下来我们看一个例题进行一下巩固。
例题1(2020江苏)梳理甲、乙两个案件的资料,张警官单独完成,分别需要2小时、8
小时;王警官单独完成需要1小时、6小时。若两人合作完成,要的时间至少是:
A.3小时
B.4小时
C.5小时
D.6小时
解析:
该题属于时间型,时间比值越小越擅长做该项工作。张警官完成甲、乙两个项目的时间之比为2:8=1:4;王警官完成甲、乙两个项目的时间之比为1:6。通过分析可知:(1:6)<(1:4),因此安排王警官完成任务甲、张警官完成任务乙。1小时后王警官完成任务甲再帮张警官完成任务乙。
赋值任务乙的工作总量为24,则张警官完成乙的效率为3,王警官完成任务乙的效率为4。王警官工作1小时完成任务甲以后,任务乙剩下的工作量为24-3脳1=21。剩下的工作量由两位警官共同完成,所需的时间为t=,所需最短总时间为3+1=4小时。
例2(2018山东选调)设有A、B两项工程,甲队单独完成A工程需要15天,单独完成B工程需要10天;乙队单独完成A工程需要5天,单独完成B工程需要15天。统筹安排甲、乙两队分工协作,以有效方式完成这两项工程,最少需要多少天?
A.7
B.7.5
C.8
D.9
解析:
该题属于时间型,时间比值越小越擅长做该项工作。甲完成A、B两个项目的时间之比为15:10=3:2;乙完成A、B两个项目的时间之比为5:15=1:3。通过分析可知:(1:3)<(3:2),因此安排乙完成任务A、甲完成任务B。5天后乙完成任务A再帮甲完成任务B。
赋值B任务的工作总量为30,则甲完成B的效率为3,乙完成任务B的效率为2。乙工作5天完成任务A以后,任务B剩下的工作量为30-3脳5=15。剩下的工作量由甲乙共同完成,所需的时间为t=,所需最短总时间为5+3=8天。
各位小伙伴,最后再给大家总结一下思维导图帮助大家理解。
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc


树图思维导图提供 埃隆·马斯克的商业版图 在线思维导图免费制作,点击“编辑”按钮,可对 埃隆·马斯克的商业版图 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:7464362ac911e8a334867bb3fc7a2346





 上海工商
上海工商