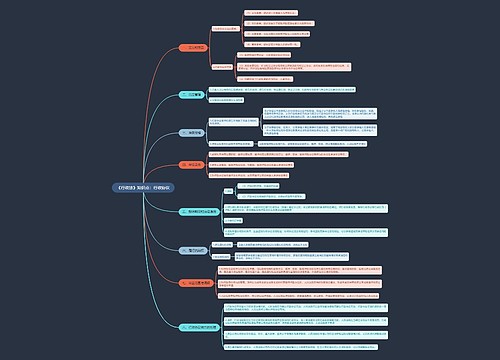
2022国考行测数量关系备考：灵活运用数字特性思维导图
在备考数量关系类题目中，倍数特性是一个重要的方法，同时也是一个秒杀的方法，但在使用的过程中有很多同学存在一些困难，尤其是面对题目往往想不到用倍数特性去解题，从而浪费了大量时间，所以今天我们来梳理一下倍数特性的具体特征和使用方法。
树图思维导图提供 2022国考行测数量关系备考：灵活运用数字特性 在线思维导图免费制作，点击“编辑”按钮，可对 2022国考行测数量关系备考：灵活运用数字特性 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：fc56d2a40c45de9f870941986acbae9d
思维导图大纲
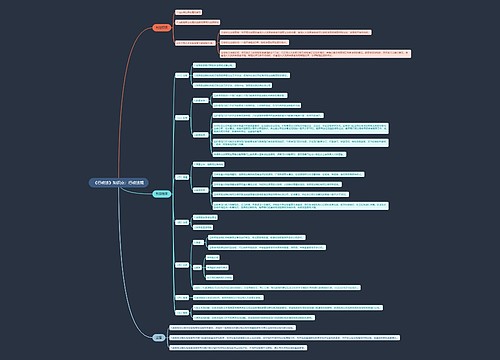
2022国考行测数量关系备考：灵活运用数字特性思维导图模板大纲
在备考数量关系类题目中，倍数特性是一个重要的方法，同时也是一个秒杀的方法，但在使用的过程中有很多同学存在一些困难，尤其是面对题目往往想不到用倍数特性去解题，从而浪费了大量时间，所以今天我们来梳理一下倍数特性的具体特征和使用方法。
倍数特性我们细分为三种题型，第一种比较简单，叫做普通倍数，这类题目特征比较明显，很容易看出来倍数关系，我们通过例题来感受一下。
例1：甲教室的人数比乙教室的7倍还多2个，那甲教室可能有多少人?
11 B. 12
C. 14 D. 16
通过这道题目我们可以得出这样的等量关系式：甲=7乙+2，所以甲的人数减去2应该是7的倍数，所以结合选项应该选择D选项，这种简单易懂而且有倍数关系的题目我们叫普通倍数。
第二种是因子倍数，形如X=abc这样的形式，如果发现要求的量含有某几个因子，则可以观察选项中的数据，把不含a，b，c这三个因子的选项排除掉，从而缩小选择的范围甚至直接选择出正确的答案。
第三种也是最常见的我们叫比例倍数，题目中也会以倍数、百分数、分数、比例的形式出现，通过两个量或者多个量形成的比例关系进而推导出数据的可能范围并结合选项选择出正确答案。比如现给出条件班级男女比例是7:4，即男：女=7:4，则可以推出以下几个结论：
1、男生人数一定是7的倍数
2、女生人数一定是4的倍数
3、总人数一定是11的倍数
4、男女之差一定是3的倍数
如果用字母代替数据得出普遍的规律为：
当a：b=m：n(m、n互质即m：n不能继续约分)
则a是m的倍数，b是n的倍数，a+b是m+n的倍数，a-b是m-n的倍数。
我们通过例题再来具体感受理解一下。
例2：在某公司年终晚会上，所有员工分组表演节目。如果按7男5女搭配分组，则只剩下8名男员工;如果按9男5女搭配分组，只剩下40名女员工。该公司员工总数为：
A. 446 B. 488
C. 508 D. 576
分析题目我们可以发现员工总数减去8应该是7+5=12的倍数，同时员工总数减去40应该是9+5=14的倍数，结合选项观察只有B符合，所以倍数特性用的好，可以快速锁定答案，事半功倍。
例3：某地举办铁人三项比赛，全程为51.5千米，游泳、自行车、长跑的路程之比为3︰80︰20。小陈在这三个项目花费的时间之比为3︰8︰4，比赛中他长跑的平均速度是15千米/小时，且两次换项共耗时4分钟，那么他完成比赛共耗时多少?
A. 2小时14分钟 B. 2小时24分钟
C. 2小时34分钟 D. 2小时44分钟
题目中有两个比例关系，第一个是路程之比，第二个是时间之比，因为题目最后求的是时间，所以我们重点看时间的比值关系，三个项目时间之比为3:8:4，我们可以得出比赛总时间应该是3+8+4=15的倍数，又因为换项耗时4分钟，所以一共耗时时间减去4为15的倍数，结合选项选择D选项
通过学习了解数字特性，我们会发现这种题目如果能够巧妙地使用数字特性的话，是可以进行秒杀的，这是一个快速解题的方法，相信同学们对数资的学习建立了一定的信心，当然，只有信心还不够，希望各位未来的局长、处长能够多加练习，熟练运用，在考场上才会有事半功倍的效果!
相关思维导图模板
树图思维导图提供 RBT工作管理计划 在线思维导图免费制作，点击“编辑”按钮，可对 RBT工作管理计划 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：07511cf9c98d75f4a7a974d65f912b8f
树图思维导图提供 分析传统文化进行创新设计的优秀作品 在线思维导图免费制作，点击“编辑”按钮，可对 分析传统文化进行创新设计的优秀作品 进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：b10e0023950f5b8b1cd58ca2e19944cc
沪公网安备 31011502019485号
上海工商