2022国考数量关系之工程问题解题技巧思维导图

笔灵AI论文写作三步搞定，GO>>

当前位置:树图

思维导图模板

资格考试

公务员考试

2022国考数量关系之工程问题解题技巧思维导图

会员免费下载或30积分

会员免费使用或30积分

旧街悲巷

浏览量：0

2023-03-04 02:35:47

已被使用0次

查看详情

工程问题是公考数量关系必考的一类题型，分清好题型分类掌握好解题方法，就可以让你拉开与对手的距离。

树图思维导图提供 2022国考数量关系之工程问题解题技巧在线思维导图免费制作，点击“编辑”按钮，可对 2022国考数量关系之工程问题解题技巧进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：81ba37d3282c6501e91292910f5f26f6

国家公务员行测备考数量关系

举报/反馈

思维导图大纲

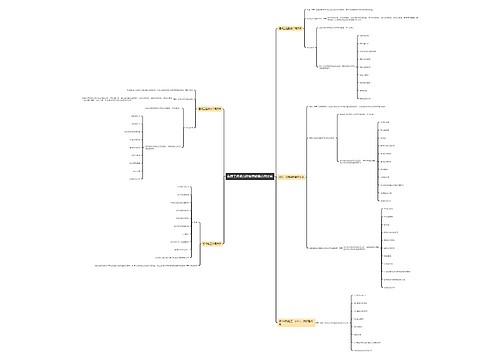
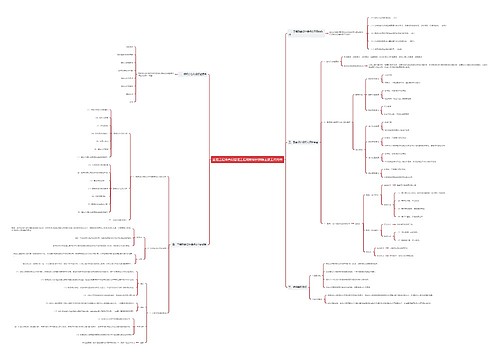
2022国考数量关系之工程问题解题技巧思维导图模板大纲

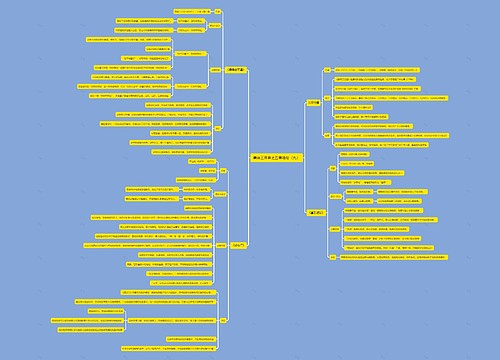
工程问题是公考数量关系必考的一类题型，分清好题型分类掌握好解题方法，就可以让你拉开与对手的距离。在日常生活中，做某一件工作，制造某种产品，完成某项工程等等，都要涉及到工作效率(e)、工作时间(t)和工作量(w)这三个量，探讨这三个数量之间关系的应用题，我们都叫做"工程问题"。

一、工程问题类型

1、给定时间型：题干中只给定工作时间。

2、效率制约型：题干中不仅给定工作时间，还给出与效率相关的某个逻辑关系。

3、给具体值型：题干中有效率、时间、总量三个量中的至少两个量的具体值。

二、答题思路

1、给定时间型：

赋总量：时间的最小公倍数(难算直接时间乘积)。

算效率：e = w / t

去求解：

2、效率制约性

赋效率：按照比例设效率，设值尽量设整数。

算总量：根据题干算总量

去求解：

3、给具体值型：代公式-列方程求解

三、例题讲解

【例题1】(2013北京)一项工程如果交给甲、乙两队共同施工，8天能完成;如果交给甲、丙两队共同施工，10天能完成;如果交给甲、丁两队共同施工，15天能完成;如果交给乙、丙、丁三队共同施工，6天就可以完成。如果甲队独立施工，需要多少天完成?

A.16 B.20

C.24 D.28

正确答案 C

解析：

题干中问的是甲独立施工需要多少天完成?审题干发现都是给出具体完成时间，所以突破点在于一定是通过时间的最小公倍数求出相关效率，然后联立求解甲的效率。

第一步：求最小公倍数

第二步：求各个式子的效率(作图表)

第三步：联立

第四步：甲独立完成需要120 梅 5 = 24天。因此，选择C选项。

【例题2】(2016春季联考)A工程队的效率是B工程队的2倍，某工程交给两队共同完成需要6天。如果两队的工作效率均提高一倍，且B队中途休息了1天，问保证工程按原来的时间完成，A队中最多可以休息几天?

A.4 B.3

C.2 D.1

正确答案 A

解析：

题干中问的是A中途最多可以休息几天?审题干发现甲的效率是乙的效率的2倍，因此效率比甲:乙 = 2:1，考虑赋值效率。

第一步：赋值效率甲 = 2、乙 = 1

第二步：计算工程总量

第三步：题干给出效率均提高一倍，因此甲 = 4、乙 = 2

第四步：设甲休息X天，得式子(作图表)

得：X = 4。因此，选择A选项。

【例题3】(2014江苏A类)甲、乙两个工程队共同修建一段长为2100千米的公路，甲队每天比乙队少修50千米，甲队先单独修3天，余下的路程与乙队合修6天完成。则乙队每天所修公路的长度是( )千米。

A.135 B.140

C.160 D.170

正确答案 D

解析：

题干中问乙队每天修公路的长度是?审题干发现没有效率之比，没有总完成时间，给出具体值，直接列方程即可。

设甲每天修X 鈥�50千米路、乙每天修X千米路，甲先干3天再与乙一起干6天，即3脳(X 鈥�50)+ 6( X + X鈥�50)= 2100千米，得：X = 170。因此，选择D选项。

结合上述三个例题来看，工程问题常考类型这三种，这里比较难的为效率制约型，很多考生很难看出隐形的效率之比，效率制约型有以下几种类型：①直接给效率之比，如甲:乙=2:1。 ②效率提升20%，那么原来的效率为1的话现在是1.2，即1:1.2 = 5:6。 ③给出50台挖掘机这种一模一样的做工工具时他们的效率都一样，按每台挖掘机效率为1来计算即可。④完成某一部分工程时甲用2天、乙用3天，即效率之比甲:乙 = 3:2。在做工程问题时比较困难的同学们可以试着作图表来解题，这种思路更清晰做题很有帮助。因此大家做工程问题的题时要抓住题型，抓住切入点很重要，是给定了时间还是有隐形的效率之比。一定要熟练掌握上述知识点并且要多做题来巩固哦。