数量关系考点实例分析:三角形两边之和大于第三边思维导图
数量关系中的几何问题近些年来一直都是高频考点,今天我们将为考生们举实例分析三角形两边之和大于第三边这一几何问题,希望通过真题讲解可以帮助备考2019国考行测的考生掌握数量关系解题技巧。
树图思维导图提供 数量关系考点实例分析:三角形两边之和大于第三边 在线思维导图免费制作,点击“编辑”按钮,可对 数量关系考点实例分析:三角形两边之和大于第三边 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:6d8dff182da9390ecf2eb6ae44339b7f
思维导图大纲
数量关系考点实例分析:三角形两边之和大于第三边思维导图模板大纲
数量关系中的几何问题近些年来一直都是高频考点,今天我们将为考生们举实例分析三角形两边之和大于第三边这一几何问题,希望通过真题讲解可以帮助备考2019国考行测的考生掌握数量关系解题技巧。
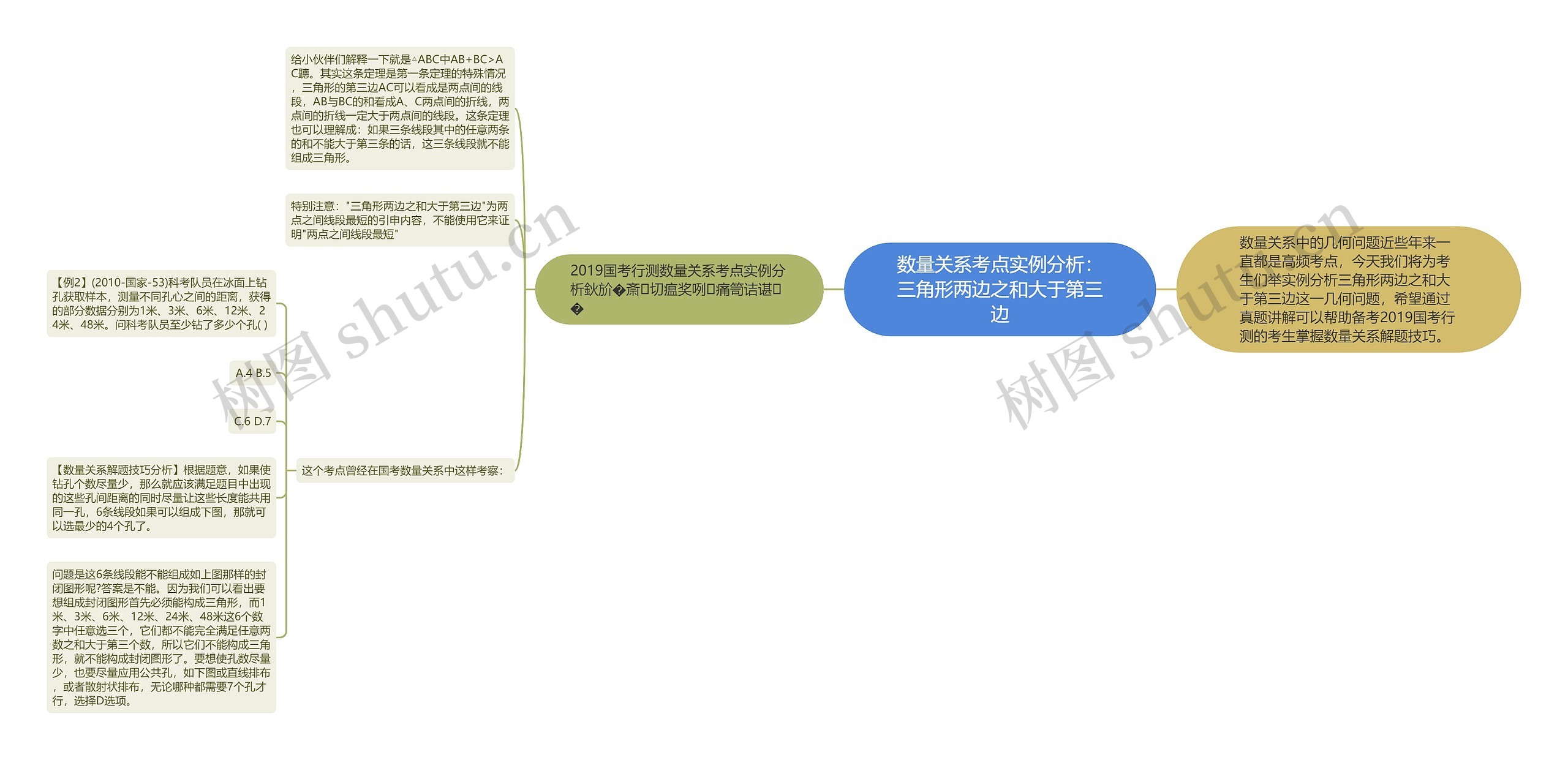
2019国考行测数量关系考点实例分析鈥斺�斎切瘟奖咧痛笥诘谌�
给小伙伴们解释一下就是△ABC中AB+BC>AC聽。其实这条定理是第一条定理的特殊情况,三角形的第三边AC可以看成是两点间的线段,AB与BC的和看成A、C两点间的折线,两点间的折线一定大于两点间的线段。这条定理也可以理解成:如果三条线段其中的任意两条的和不能大于第三条的话,这三条线段就不能组成三角形。
特别注意:"三角形两边之和大于第三边"为两点之间线段最短的引申内容,不能使用它来证明"两点之间线段最短"
这个考点曾经在国考数量关系中这样考察:
【例2】(2010-国家-53)科考队员在冰面上钻孔获取样本,测量不同孔心之间的距离,获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔( )
A.4 B.5
C.6 D.7
【数量关系解题技巧分析】根据题意,如果使钻孔个数尽量少,那么就应该满足题目中出现的这些孔间距离的同时尽量让这些长度能共用同一孔,6条线段如果可以组成下图,那就可以选最少的4个孔了。
问题是这6条线段能不能组成如上图那样的封闭图形呢?答案是不能。因为我们可以看出要想组成封闭图形首先必须能构成三角形,而1米、3米、6米、12米、24米、48米这6个数字中任意选三个,它们都不能完全满足任意两数之和大于第三个数,所以它们不能构成三角形,就不能构成封闭图形了。要想使孔数尽量少,也要尽量应用公共孔,如下图或直线排布,或者散射状排布,无论哪种都需要7个孔才行,选择D选项。
相关思维导图模板


树图思维导图提供 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 在线思维导图免费制作,点击“编辑”按钮,可对 904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

树图思维导图提供 第六章 群体传播与组织传播_副本 在线思维导图免费制作,点击“编辑”按钮,可对 第六章 群体传播与组织传播_副本 进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1672f555831e7d9a3bb2cf2fb792cb49










 上海工商
上海工商